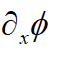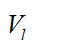dsaun777 said:
Invariants are built out of components and bases, but aren't the bases "vectors" themselves and should be considered invariant?
Of course each basis is a set of invariant vectors, but if you change the basis you change it, right?
As an example take a Euclidean ##\mathbb{R}^2## and the change from a Cartesian basis to standard polar-coordinate basis (not holonomous but the usual orthonormal basis). The Cartesian basis is convenient, because the basis is constant over the entire plane. Let's call this basis ##\vec{e}_i## (##i \in \{1,2 \}##) and the bases of polar coordinates, which are dependent on the point on the plane ##\vec{e}_i'(r,\vartheta)##. For the position vector we write ##\vec{r}=x^i \vec{e}_i = x \vec{e}_1 + y \vec{e}_2##. Then for any vector field you have
$$\vec{V}(\vec{r})=\vec{e}_i V^i(x,y) = \vec{e}_j'(r,\vartheta) V^{\prime j}(r, \vartheta).$$
To get the components of the position vector in the polar-coordinate basis we note that
$$x=r \cos \vartheta, \quad y=r \sin \vartheta$$
and thus
$$\partial_r \vec{r}=\cos \vartheta \vec{e}_1 + \sin \vartheta \vec{e}_2 \; \Rightarrow \; g_r=|\partial_{r} \vec{r}|=1$$
and
$$\partial_{\vartheta} \vec{r}=-r \sin \vartheta \vec{e}_1 + r \cos \vartheta \vec{e}_2 \; \Rightarrow\; g_{\vartheta}=|\partial_{\vartheta} \vec{r}|=r.$$
Thus we have
$$\vec{e}_1'(r,\vartheta)=\frac{1}{g_r} \partial_r \vec{r}=\cos \vartheta \vec{e}_1 + \sin \vartheta \vec{e}_2, \quad \vec{e}_2'(r,\vartheta)=\frac{1}{g_\vartheta} \partial_{\vartheta} \vec{r} = -\sin \vartheta \vec{e}_1 + \cos \vartheta \vec{e}_2.$$
Now we have
$$\vec{e}_j'(r,\vartheta)=D_{ij}(r,\vartheta) \vec{e}_i$$
with the transformation matrix (which is here of course orthogonal, because we change between orthonormal bases)
$$D_{ij}(r,\vartheta)=\vec{e}_i \cdot \vec{e}_j' \; \Rightarrow \; \hat{D}=\begin{pmatrix} \cos \vartheta & -\sin \vartheta \\ \sin \vartheta & \cos \vartheta \end{pmatrix}.$$
The transformation of the vector components thus follows from
$$V^{\prime j} \vec{e}_j' = V^{\prime j} D_{ij} \vec{e}_i \; \Rightarrow \; V^{i}=D_{ij} V^{\prime j}.$$
Now it's easy to derive the usual vector operators on scalar and vector-field components. So let ##\Phi## be a scalar field. Then the gradient is defined by
$$\mathrm{d} \Phi=\mathrm{d} x^i \partial_i \Phi:=\mathrm{d} \vec{r} \cdot \vec{\nabla} \Phi.$$
Since this is still a scalar, ##\vec{\nabla} \Phi## must be a vector field. Denoting ##q^1=r## and ##q^2=\vartheta## we have
$$\mathrm{d} \Phi=\mathrm{d} q^j \frac{\partial}{\partial q^j} \Phi = \mathrm{d} q^j \frac{\partial \vec{r}}{\partial q^j} \cdot \vec{\nabla} \Phi.$$
Writing this out leads to
$$\mathrm{d} \Phi=(\mathrm{d} r g_r \vec{e}_1' + \mathrm{d} \vartheta g_{\vartheta} \vec{e}_2') \cdot \vec{\nabla} \Phi=\mathrm{d}_r \frac{\partial \Phi}{\partial r} + \mathrm{d} \vartheta \frac{\partial \Phi}{\partial \vartheta}$$
and thus
$$(\nabla \Phi)^{'1}=\frac{1}{g_r} \partial_r \Phi=\partial_r \Phi, \quad (\nabla \Phi)^{'2}=\frac{1}{g_{\vartheta}} \partial_{\vartheta} \Phi=\frac{1}{r} \partial_{\vartheta} \Phi.$$
For vector fields one has to be careful to take into account the dependence of the basis vector on the generalized coordinates. The most elegant method to get the expressions of the operators ##\text{div}## and ##\text{curl}## is to use their coordinate independent definitions through integrals. Another way is to use the simple expressions in Cartesian coordinates and transform them appropriately. For the divergence of a vector field we have
$$\mathrm{div} \vec{V}=\vec{\nabla} \cdot \vec{V}=\frac{\partial}{\partial x^i} V^i = \frac{\partial}{\partial x^i} D_{ij} V^{\prime j}=\frac{\partial q^k}{\partial x_i} \frac{\partial}{\partial q_k} D_{ij} V^{\prime j}.$$
Now we need the Hesse matrix
$$H_{ki}=\frac{\partial q^k}{\partial x_i}$$
which is inconvenient to calculate. We rather use its inverse defining
$$\tilde{H}_{ab}=\frac{\partial x^a}{\partial q^b}.$$
Indeed from
$$\frac{\partial x^a}{\partial x_b}=\delta_{ab} = \frac{\partial x_a}{\partial q_c} \frac{\partial q_c}{\partial x_b} = \tilde{H}_{ac} H_{cb}$$
we see that in matrix notation ##H=\tilde{H}^{-1}##. Now
$$\tilde{H}=\begin{pmatrix}\cos \vartheta & -r \sin \vartheta \\ \sin \vartheta & r \cos \vartheta\end{pmatrix}.$$
Then
$$H=\tilde{H}^{-1} =\frac{1}{r} \begin{pmatrix} r \cos \vartheta &r \sin \vartheta \\ -\sin \vartheta & \cos \vartheta \end{pmatrix}.$$
After some algebra one finally gets
$$\text{div} \vec{V}=\frac{1}{r} \partial_r (r V^{\prime 1}) + \frac{1}{r} \partial_{\vartheta} V^{\prime 2}.$$
The curl can be calculated in a similar way, though it's even more cumbersome ;-)).