Transformation of the Christoffel Symbols

[Luke Tan]

TL;DR Summary

Derivation of the transformation rules for the Christoffel symbols.

In Landau Book 2 (Classical Field Theory & Relativity), he mentions that the transformation rules of the christoffel symbols can be gotten by "comparing the laws of transformation of the two sides of the equation governing the covariant derivative"

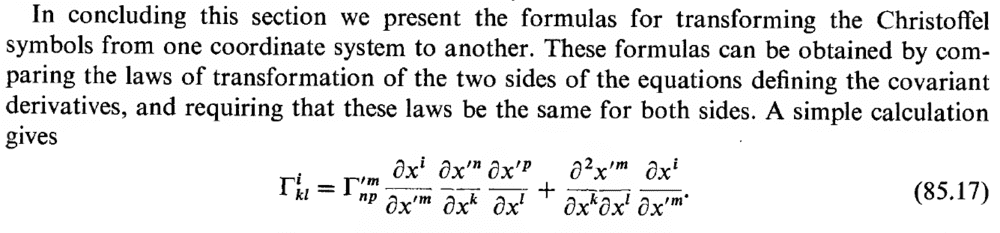
I would believe that by the equations defining the covariant derivative, he means
$$DA^i = (\frac{\partial A^i}{\partial x^l} + \Gamma^i_{kl}A^k)dx^l$$
$$DA_i = (\frac{\partial A_i}{\partial x^k} + \Gamma^k_{il}A_k)dx^l$$

In addition, I would believe that he wants me to use the transformation rules
$$A^i = \frac{\partial x^i}{\partial {x'}^k}{A'}^k$$
$$A_i = \frac{\partial {x'}^k}{\partial x^i}{A'}_k$$However, when attempting to transform the definitions of the covariant derivative from one coordinate system to another, I ran into the following problem - how does the covariant derivative transform? It clearly transforms like a tensor, but does it transform like a covariant tensor, a contravariant tensor, or a mixed one?

So, my questions are:
1. How does a covariant derivative transform? Is it possible to use this to prove the statement that Landau wants to prove?
2. If not, how else would I show this transformation rule for the Christoffel symbols?

 

[Orodruin]

Summary: Derivation of the transformation rules for the Christoffel symbols.

It clearly transforms like a tensor, but does it transform like a covariant tensor, a contravariant tensor, or a mixed one?

It depends on what you are taking the derivative of. As the name suggests, the covariant derivative adds one covariant index.

I would believe that by the equations defining the covariant derivative, he means

Careful with the signs!

 

[Engie]

$$DA_i=(\frac{∂A_i}{∂x^k}+ \Gamma^k_{il}A_k)dx^l$$

This sign is wrong and one index (probably a typo). In Pavel Grinfeld's Introduction to Tensor Analysis and the Calculus of Moving Surfaces, the covariant derivative of a covariant tensor is:

$$\nabla_k A_i=\frac{∂A_i}{∂x^k} - \Gamma^l_{ik}A_l$$

The covariant derivative of a contravariant tensor is:

$$\nabla_k A^i=\frac{∂A^i}{∂x^k} + \Gamma^i_{lk}A^l$$

The covariant derivative $\nabla_k$ acts exactly as a covariant tensor. The contravariant derivative $\nabla^k$ is defined as

$$\nabla^k= g^{kj} \nabla_j$$

and acts as a contravariant tensor.

The transformation rule of the Christoffel Symbol in a flat space can be derived from the identity:

$$ \Gamma^k_{ij} = \frac{\partial \vec{x}_i}{\partial x^j} \cdot \vec{x}^k $$

by applying the change of coordinates and the product rule.

 

[Luke Tan]

So far, I have the definition of the covariant derivative in both the primed and unprimed coordinate systems
$$A_{i;l}'=\frac{\partial {A'}_i}{\partial {x'}^l}-{\Gamma'}^k_{il}{A'}_k$$
$$A_{i;l}=\frac{\partial A_i}{\partial x^l}-{\Gamma'}^k_{il}A_k$$

On the left hand side, we use the transformation rules for a covariant tensor

$$A_{i;l}=\frac{\partial {x'}^l}{\partial x^i}\frac{\partial {x'}^m}{\partial x^k}{A'}_{l;m}$$

On the right hand side, we can have similar transformation rules
$$\frac{\partial A_i}{\partial x^l} = \frac{\partial {x'}^l}{\partial x^i}\frac{\partial {x'}^m}{\partial x^k}\frac{\partial {A'}_l}{\partial {x'}^m}$$

$${\Gamma'}^k_{il}{A'}_k=\frac{\partial {x'}^l}{\partial x^i}\frac{\partial {x'}^m}{\partial x^k}{\Gamma'}^k_{lm}A_k$$

However,when equating these two it seems like the $\frac{\partial {x'}^l}{\partial x^i}\frac{\partial {x'}^m}{\partial x^k}$ terms can just be factorised and cancelled, to give the definition of the covariant derivative in the unprimed coordinates. I don't seem to be getting any closer to the answer that i want.

Can someone give me a hint please?

Thanks!

 

[Antarres]

Your problem is that you think partial derivative of a vector field, transforms the same as (1,1) tensor field(or (0,2) in case vector field was covariant vector field), which is wrong. In fact that would be the reason we introduce covariant derivative in the first place.
So to correct you, we have:
$$\frac{\partial A'_i}{\partial x'^j} = \frac{\partial x^k}{\partial x'^j} \frac{\partial}{\partial x^k}A'_i = \frac{\partial x^k}{\partial x'^j} \frac{\partial}{\partial x^k}\left(\frac{\partial x^l}{\partial x'^i}A_l\right)$$

Now you see when you act with that partial derivative above, you will get, not just the normal tensor transformation law, but also the extra term. When we introduce Christoffel symbols, their transformation is designed so that covariant derivative would actually transform like you assumed normal partial derivatives do. So in their transformation law, they compensate for this extra term. Hope that helps some.