Circle Theorems: Solving for Unknown Angles in Isosceles Triangles

[grahammm]

Hi,

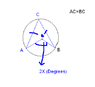
I am really confused with circle theorems, attached is a diagram and I need to find out ABC and CBO.

I have worked out that angle ACB is x degrees, and also know that angle OAC is equal to angle OBC.

But I don't know how to work out the what either are

Thanks

Graham

 

[grahammm]

Is this something to do with opposite angles on a cyclic quadratic add up to 180?

 

[whozum]

If youcan post it on the web somewhere, we'd be able to see it before tomorrow. It has to be pre approved.

 

[grahammm]

See www.kgmm.co.uk/maths.GIF[/URL]

Many thanks!

Graham

 

[whozum]

I am really confused with circle theorems, attached is a diagram and I need to find out ABC and CBO.

Arc ABC? Angle ABC? You didnt label this angle.


Do you know anything specific about the inscription of the triangle in the circle? I want to say that the arcs between A B and C are 120 degrees, but I can't tell if that's whatits supposed to be.

 

[grahammm]

Find in terms of X, expressions for the angles:

- ABC
- CBO

The points A,B, and C lie on the centre circle O.

 

[whozum]

Since AC = BC, the triangle ABC is isosceles, and angles ABC and BAC are equal. The sum of all three angles is 180.
Where y is angle ABC
180 = 2y+x
y = 90-x/2

Do you have the answer?