VinnyCee
- 486
- 0
Using superposition, find v_0 in the following circuit.
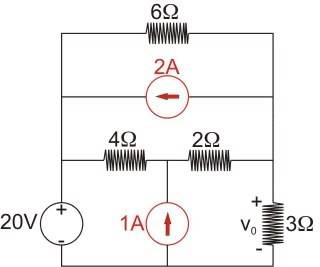
My work so far:
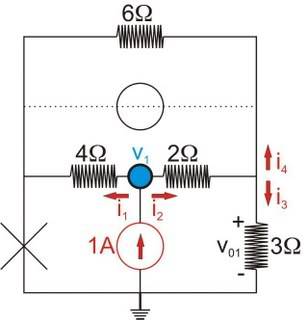
v_1\,=\,2\,i_2\,+\,v_{0\,1}
v_1\,=\,4\,i_1
v_{0\,1}\,=\,3\,i_3
v_{0\,1}\,=\,6\,i_4
KCL @ v1:
1\,A\,=\,i_1\,+\,i_2
i_2\,=\,i_3\,+\,i_4
Using these six equations, with 6 variables:
v_{0\,1}\,=\,\frac{12}{7}\,V
Is that correct?
My real question is how to put the six equations above into matrix form to enable solving using RREF.
Thanks
EDIT: I have fixed this part with Paallikko's guidance (thanks!)
i_1\,=\,\frac{1}{4}\,v_1
i_2\,=\,\frac{1}{2}\,v_1\,-\,\frac{1}{2}\,v_{01}
i_3\,=\,\frac{1}{3}\,v_{01}
i_4\,=\,\frac{1}{6}\,v_{01}
i_1\,+\,i_2\,=\,1\,A\,\,\,\Rightarrow\,\,\,\frac{3}{4}\,v_1\,-\,\frac{1}{2}\,v_{01}\,=\,1
i_3\,+\,i_4\,=\,i_2\,\,\,\Rightarrow\,\,\,\frac{1}{3}\,v_{01}\,+\,\frac{1}{6}\,v_{01}\,=\,\frac{1}{2}\,v_1\,-\,\frac{1}{2}\,v_{01}
v_{01}\,=\,1\,V
My work so far:
v_1\,=\,2\,i_2\,+\,v_{0\,1}
v_1\,=\,4\,i_1
v_{0\,1}\,=\,3\,i_3
v_{0\,1}\,=\,6\,i_4
KCL @ v1:
1\,A\,=\,i_1\,+\,i_2
i_2\,=\,i_3\,+\,i_4
Using these six equations, with 6 variables:
v_{0\,1}\,=\,\frac{12}{7}\,V
Is that correct?
My real question is how to put the six equations above into matrix form to enable solving using RREF.
Thanks
EDIT: I have fixed this part with Paallikko's guidance (thanks!)
i_1\,=\,\frac{1}{4}\,v_1
i_2\,=\,\frac{1}{2}\,v_1\,-\,\frac{1}{2}\,v_{01}
i_3\,=\,\frac{1}{3}\,v_{01}
i_4\,=\,\frac{1}{6}\,v_{01}
i_1\,+\,i_2\,=\,1\,A\,\,\,\Rightarrow\,\,\,\frac{3}{4}\,v_1\,-\,\frac{1}{2}\,v_{01}\,=\,1
i_3\,+\,i_4\,=\,i_2\,\,\,\Rightarrow\,\,\,\frac{1}{3}\,v_{01}\,+\,\frac{1}{6}\,v_{01}\,=\,\frac{1}{2}\,v_1\,-\,\frac{1}{2}\,v_{01}
v_{01}\,=\,1\,V
Last edited: