Circuits Q&A: My Question About Vdb

  • Thread starter Thread starter Miike012
  • Start date Start date
  • Tags Tags
    Circuits
AI Thread Summary
The discussion centers on the relationship between Vbd and Vdb in the context of charge flow. It asserts that Vbd equals VR2, indicating that current from point d to point b gains potential energy. However, the original poster questions this interpretation, noting that electrons, which flow opposite to conventional current, lose potential energy when moving from lower to higher potentials. This leads to the conclusion that Vbd should actually equal -VR2. Clarification is sought on this apparent contradiction regarding the behavior of electrons and potential energy.
Miike012
Messages
1,009
Reaction score
0
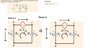
My question is regarding Vdb.
for pos flow of charge

Vbd = -Vdb
and
Vdb = -VR2
so Vbd = VR2.

This means that the current flowing from point d to point b gained potential energy. However the flow of charge from d to b are electrons and electrons lose potential energy as they move from lower to higher potentials. So when I look at it in that point of view
Vbd should be equal to -VR2.

Can someone clarify to me why I am wrong.
 

Attachments

  • Pp.jpg
    Pp.jpg
    19.8 KB · Views: 382
Physics news on Phys.org
Electrons are negatively charged, and flow in the opposite direction of the current.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

How does a simple circuit work?
Replies
12
Views
1K
Understanding Inductance and Induced EMF in Simple Circuits
Replies
49
Views
3K
Write boolean expression describing this circuit
Replies
4
Views
1K
Determining Inductance L in an LC Circuit
Replies
5
Views
2K
Current through an inductor as a function of time
Replies
10
Views
373
Understanding example in Wikipedia entry for open circuit voltage
Replies
3
Views
2K
Minimizing the Energy of Two Conductors Very Far Apart
Replies
23
Views
2K
How to determine if electrical components are connected in parallel or in series?
Replies
10
Views
949
Final Charge of a Capacitor in a Circuit with Capacitors and Resistors
Replies
9
Views
2K
Polarities of capacitor plates in a complex circuit
Replies
14
Views
2K

Hot Threads

Recent Insights

Back
Top