GreenPrint
- 1,186
- 0
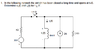
Circuits Question -- Voltage and current in an inductor circuit
See Attached
I found Zeq and there are exactly 2 Amps going into it. I'm not sure what to do from here.
Z_{eq} = \frac{<(arctan(\frac{R}{ωL}))}{ω^{2}L^{2}+R^{2}}
I'm not sure what to do from here, thanks for any help.
Homework Statement
See Attached
Homework Equations
The Attempt at a Solution
I found Zeq and there are exactly 2 Amps going into it. I'm not sure what to do from here.
Z_{eq} = \frac{<(arctan(\frac{R}{ωL}))}{ω^{2}L^{2}+R^{2}}
I'm not sure what to do from here, thanks for any help.