- #1
jjiimmyy101
- 74
- 0
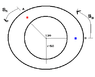
Two cyclists A and B, are traveling counterclockwise around a circular track at a constant speed of 8 ft/sec at the instant shown. If the speed of A is increased at aA = SA ft/sec^2, where SA is in ft, determine the distance measured counterclockwise along the track from B to A between the cyclists when time is = 1 sec. What is the magnitude of the acceleration of each cyclist at the instant?
To find the length of an arc, you use the equation arc=theta*radius, but how do you encorporate the time into this? I don't know how far cyclist A moves.
To find the magnitude of acceleration you can use the sqrt of a(normal)^2 + a(tangential)^2.
aB =1.28 ft/sec^2
because a(tangential)=0 (constant velocity) and a(normal)=64/50
I don't know what aA is equal to.
Any suggestions?
I posted a picture too.
To find the length of an arc, you use the equation arc=theta*radius, but how do you encorporate the time into this? I don't know how far cyclist A moves.
To find the magnitude of acceleration you can use the sqrt of a(normal)^2 + a(tangential)^2.
aB =1.28 ft/sec^2
because a(tangential)=0 (constant velocity) and a(normal)=64/50
I don't know what aA is equal to.
Any suggestions?
I posted a picture too.
Attachments
Last edited: