hannam
- 10
- 0
Homework Statement
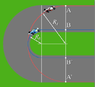
In Formula 1 race, the cars approach curves
from the outside, cut through to the inside, and
then drift again to the outside (red path AA’ in the
figure). However, the blue path (BB’) in the figure
is shorter. Then why do not the drivers follow the
shortest path? Give answer to this question by
proving that tred (time to travel red path) is shorter
than tblue (time to travel blue path). Only given
values are RA = 32 m and RB = 10 m, and static
friction coefficient of the road is
μs =1.2. Assume
cars make motion with constant speed throughout
the path.
Important: The speeds of the cars do not change
due to static or kinetic frictions. However, only
static friction acts to the car as a centripetal force when the car makes a circular motion.
Therefore, first find maximum possible speed of a car while making a circular motion.
Homework Equations
m.g.μs=m.V2/r
T= 2∏r/V
The Attempt at a Solution
I tried m.g.μs=m.V2/r equation and found V max values for both cars (19,3 for the car on the red path and 10.8 for the blue path)
and then for T values i used equation 2∏r/V and found T for blue path is shorter. but in the question it wants me to prove that tred is shorter :/
i attached the picture of question.
where am i wrong? thanks for helpp!