Circular + Projectile Motion question

[Carbon123]

Homework Statement

A ball was placed in a frictionless circular track with radius R and given initial velocity of u.The ball went around the cricle ,left at some point,then arrived in the same initial position after undergoing projectile motion.
a.State the speed u in terms of R and g
b.Coordinate of the ball when it left the circle.

Homework Equations

Conservation of energy
F=mv^2/R

The Attempt at a Solution

I assumed that the ball left at angle theta with the horizontal from the circle.therefore ,its height is R(1+sin(x)) then the ball takes off,the normal force is 0.Therefore speed at takeoff is v = gRsin(x).Using conservation of energy i was able to get u=gR(2+3sin(x)

From this point on I am kind of stuck to find the angle x ,and I do not know how to solve it.I tried to analyze the projectile motion,but i am still stuck.Help please ?
Thanks in advance

 

[TSny]

Does the ball start at the bottom of the circle?

Using conservation of energy i was able to get u=gR(2+3sin(x)

Clearly there is a mistake in this formula. The units for the left and right sides don't match and the parentheses don't match.

But, I think you're on the right "track".

From this point on I am kind of stuck to find the angle x ,and I do not know how to solve it.I tried to analyze the projectile motion,but i am still stuck.Help please

Show us what you did with the projectile motion.

 

[Carbon123]

Oh I forgot to write that it starts from the bottom of the circle,and that its intial position is the center of coordinate.The u equation should be u^2 =gR(2+3sin (x))then sin(x)=(u^2-2gR)/3gR.So we know the value of sin (x).I put 0 =Yo+gRsin(x)cosxt-(1/2)gt^2.and 0=X-gRsin(x)sinx.t Is this true and then I would find x and yo respectively ?

 

[Carbon123]

I am terribl sorry,I am so confused right now ,but will it possible if we just have Y=R(1+sinx) and x=R cosx ? This is confusing...

 

[TSny]

Oh I forgot to write that it starts from the bottom of the circle

OK, good.

and that its intial position is the center of coordinate.

So, the origin of the x-y coordinate system is at the bottom of the circle?

The u equation should be u^2 =gR(2+3sin (x))

OK. But I think it would be a good idea to use a different symbol for the angle. Click on the Σ symbol on the tool bar to obtain some mathematical symbols like θ.

I put 0 =Yo+gRsin(x)cosxt-(1/2)gt^2.and 0=X-gRsin(x)sinx.t

These equations are not correct. Note that the middle term of the y equation does not have units of distance. The last term of the x equation does not have the units of distance.

In your first post you stated that the take off speed is v = gRsin(x). Can this be correct? Check units.

 

[TSny]

I am terribl sorry,I am so confused right now ,but will it possible if we just have Y=R(1+sinx) and x=R cosx ? This is confusing...

OK, these would be the coordinates of the take-off point. You can see how confusing it is to use x for both the x coordinate and the angle of the radius of the circle at the take-off point.

 

[UchihaClan13]

The first logical step would be to presume that the ball covers a major portion of the circular track so as to simplify the projectile motion calculations
And how did you get v=gRsinx?
Your L.H.S has units of metre/second while your R.H.S has units of Metre^2/Second^2

UchihaClan13

 

[UchihaClan13]

What do you mean when you say "the center of coordinate"
Does this refer to a specific set of coordinates or is this trivial?UchihaClan13

 

[UchihaClan13]

DO you mean the center to be the origin(the starting point of the ball would then have the coordinates 0,-R)UchihaClan13

 

[Carbon123]

Oh,my mistake,v=(gR sin(x))^½.so what should i do next ? The center coordinate means that the ball's initial position is the (0,0) coordinate

 

[TSny]

Oh,my mistake,v=(gR sin(x))^½.

OK

so what should i do next ?

Use this correct expression for v in your projectile equations for x and y. Since you are not interested in the time, you could try to eliminate t.

 

[UchihaClan13]

Oh,my mistake,v=(gR sin(x))^½.so what should i do next ? The center coordinate means that the ball's initial position is the (0,0) coordinate

Okay dokie
I'll just check your expression but dimensionally,it's correct
Now,use the equation of trajectory to determine your final coordinates
And also remember energy conservation
P.S.A hint: choose your coordinate axeses carefully
UchihaClan13

 

[Carbon123]

Equation of parabola is
y=yo+(gR sin (x))^½sin(90-x)t-1/2 gt^2
x=xo-gRsin(x)cos(90-x)t
Where xo is takeoff point
Then y =0 and x =0 ,and then substitute the t from the second equation but then I have two unknowns that is Xo and Yo which i am looking for ? (Help needed)

 

[TSny]

Equation of parabola is
y=yo+(gR sin (x))^½sin(90-x)t-1/2 gt^2
x=xo-gRsin(x)cos(90-x)t

May I rewrite these two equations using the symbol θ for the angle? Then you would have

y=yo+(gR sin (θ))^½sin(90-θ)t-1/2 gt^2
x=xo-gRsin(θ)cos(90-θ)t

I think you left out a square root in the second equation. Otherwise, the equations look good.
There are trig identities that allow you to write sin(90-θ)t and cos(90-θ) in a simpler way.

Then y =0 and x =0 ,and then substitute the t from the second equation

Yes.

but then I have two unknowns that is Xo and Yo which i am looking for ? (Help needed)

But you can express Xo and Yo in terms of R and θ.

 

[mukundpa]

a.State the speed u in terms of R and g
b.Coordinate of the ball when it left the circle.
I think there is no need to solve any projectile motion because the coordinate of the point where ball leaves the circle are required and before it is moving in circular path.
Part a need the range of the velocity u for which the ball leaves the circle and make a projectile motion. For that the ball should go above the horizontal level from the center of the circle and should not complete the circle and for that sqrt(2gR) < u < sqrt (5gR)
For part b we have to find the point where the ball leaves the track (if u is appropriate) and that is the point where the reaction of the track on the ball just become zero. we may solve this in terms of angle and than geometrically calculate x and y coordinate of this point..

 

[TSny]

I think there is no need to solve any projectile motion because the coordinate of the point where ball leaves the circle are required and before it is moving in circular path.

I don't see how to avoid working with the projectile motion equations.

Part a need the range of the velocity u for which the ball leaves the circle and make a projectile motion. For that the ball should go above the horizontal level from the center of the circle and should not complete the circle and for that sqrt(2gR) < u < sqrt (5gR)
For part b we have to find the point where the ball leaves the track (if u is appropriate) and that is the point where the reaction of the track on the ball just become zero. we may solve this in terms of angle and than geometrically calculate x and y coordinate of this point..

WinstonC has already found an expression for the speed at the moment the object leaves the track in terms of where it is on the track:
v = √(Rgsinθ). See post #10. θ is the unknown angle that the radius of the circle makes to the horizontal at this point of the circle. (He used x to denote this angle.)

He has already found expressions for the x and y coordinates of the initial point of the projectile motion in terms of R and θ. See post #4.

He has also set up the projectile motion equations. He just needs to bring all this together and do some algebra.

 

[Carbon123]

So which method should I do ?I am leaning towards mukundpa's approach because it seems much easier ,but that means we ignore the projectile motion completely and just assume that it leaves the track at speed √(2gR)<v<√(5gR) because that's the point where it is possible to complete a projectile motion ? and I already found the θ angle that is = (u^2-2gR)/3gR and then substitute it to yo=R(1+sin θ) and x =R cosθ ? That's it ?

 

[mukundpa]

Let the velocity of the ball is v when it leaves the circle and its radius at that time is making angle θ with the upward vertical. Than the velocity v is given by conservation of energy as
v² = u² - 2gR(1+ cosθ)
At the point it leaves the track the normal reaction of the track just becomes zero thus the radial component of weight gives the required centripetal force and thus we get
mv²/R = mg cosθ
from above two equation we can eliminate v² and solve for θ in terms of u. and knowing θ coordinate of the point it leaves will be
x = R sin θ and
y = R (1 + cos θ)
Hope I am thinking in correct way. The angle and thus the coordinates depends on u and thus will be in terms of u.

 

[Carbon123]

Could you care to explain why we ignored the projectile motion ? Did we consider it only on the a part of the question ? Thanks

 

[TSny]

v² = u² - 2gR(1+ cosθ)
...
mv²/R = mg cosθ
...
x = R sin θ and
y = R (1 + cos θ)
Hope I am thinking in correct way. The angle and thus the coordinates depends on u and thus will be in terms of u.

Yes, all of that is good. But you still need to find the particular value of u that will give a projectile motion trajectory that passes through the origin (x,y) = (0,0). At least that's how I'm interpreting the wording of the problem.

You are taking θ as measured from the vertical, whereas WinstonC and I were taking the angle to be measured from the horizontal. But that's ok.

 

[mukundpa]

If the ball is directly returning to the initial position position after the projectile motion than we may consider it as a projectile at the point it leaves the circle with velocity v and angle θ to the horizontal and then we can use equation of trajectory. Plugging the values of v and θ we can get the value of u for which it will hit the initial position directly otherwise it will strike some other point of the track and will come to the initial point,
-y = (-x) tanθ - g(-x)²/2v²cos²θ

 

[Carbon123]

So i take the θ from the two equations and equal the with the theta from conservation of energy ,and then I will know its speed ?(in g and R) and its intial position can be found by Rcos and R sin respectively using either of the equation for theta ?.How do you solve for theta in the parabolic equation y=xtanθ-gx^2/(2v^2 cos^2θ).What is the y and x ? Is it 0 and 0 ? Or do we need to add yo xo as initial position (where it left ) ?

 

[ehild]

So i take the θ from the two equations and equal the with the theta from conservation of energy ,and then I will know its speed ?(in g and R) and its intial position can be found by Rcos and R sin respectively using either of the equation for theta ?.How do you solve for theta in the parabolic equation y=xtanθ-gx^2/(2v^2 cos^2θ).What is the y and x ? Is it 0 and 0 ? Or do we need to add yo xo as initial position (where it left ) ?

You almost solved the problem by yourself, and in case you had made a drawing and explained the notations correctly, you would have done.
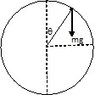
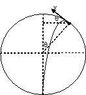
You have the set-up, as in the figure. The ball starts from the origin, with speed u. It moves along the circle of radius R, till the radial component of gravity is less than the centripetal force, and some inward force is needed from the track. When the normal force is zero, the ball leaves the track and moves like a projectile along the orange line.
You said that you assumed that the ball left at angle theta with the horizontal from the circle, but worked with the angle the velocity made with the vertical. You can determine the coordinates in terms of that angIe.
The ball left the track at point P(x₀,y₀) with velocity V₀, tangent to the circle. It encloses the angle θ with the horizontal in the figure.

You have determined the speed when the ball left the track by equating the centripetal force by the normal component of gravity but you calculated as if θ was the angle the velocity enclosed with the vertical.
You also used conservation of energy to get the relation between u and Vo: 1/2(u²-V₀²)=gy₀
Leaving the track at P, the ball performs projectile motion. In Post #13 you wrote the x and y coordinates of the projectile but you have forgotten that x₀ and y₀ were the coordinates of P, the initial point of the projectile. That was your idea to solve the problem and it was correct.
The ball returns to the origin, x=0, y=0. From the equation of motion, x-x₀=V_0xt, y-y₀=V_0yt-g/2 t², you know x and y, and you can express x₀ and y₀ with θ and R, and you know Vo in terms of g, R and θ, so you can find θ from these equations. Your equations were almost correct :)
Start again, using the angle θ shown in the figure, and do not forget the square roots.