Classic E&M Problem: Analyzing Point Charge & Charged Sphere

[turnerre]

A general problem you run into during an E&M class is the one involving a point charge a distance from a charged sphere. In cases where the point is far enough away from the sphere, the system can be treated like two points.

In my case I have a point charge "q" a distance "z" away from the center of a sphere of radius "R." The distance is not big enough for the system to be considered as two points of charge.

When asked to solve for the potential or the E-field at the point charge usually one just integrates across the sphere while accounting for different distances (i.e. distance from point charge to dq on sphere) from the point charge to the "dq's" they are integrating.

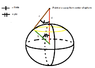
My question is what form of integration would be easiest? I have it down to four types of integrating. It helps to use this picture to visualize each integration, there is an attached file/drawing of the sphere and the rings that are integrated.

The first would be to integrate using the distances z and R to solve for some "r" (the distance from point z to the dq) and then integrate across a ring and then the sphere.

The second involves integrating the rings using a distance "x" which is the distance from the center of the sphere to the height of the ring in the z direction. For example the distance x when the specific dq is on the point closest to point z would be z-R. Likewise the furthest dq would be z+R.

The third integration method would be to use a distance "tau" which is the distance from the z axis to the dq ring. In the picture that would be R*sin(phi). Using this tau one could integrate from -R to R to solve for the e-field.

The fourth form of integration I would believe to be the hardest... Integrate with respect to an angle. The angle would be the one formed by the point z and the line connecting point z to a charge dq. This would be hard because you would have to integrate to a point where the line between dq and point z is tangent to the sphere. Then you would have to integrate a second time for all the points after that tangent point.

So which integration is the easiest?... I was given a hint that the first one is not the easiest although it is the most common.

The idea of this problem is to make you attack a problem from all possible points so in the future you may understand the easier/possibly faster way of calculating things.

 

[chrisk]

If a sphere with radius "R" is a conductor then the charge is on the surface. The E field produced by the ring along the z axis is

dE_z=K\frac{\sigma{}2\pi{}R\sin{\phi}Rd\phi}{r^2}\cos{\theta}

where sigma is the surface charge density, Rsin(phi) is the ring radius, and Rd(phi) is the ring width. The distance, r², can be expressed in terms of phi, z, and R using the law of cosines. Due to symmetry, only the z component of the field contributes so this component is determined using cosine of theta, which can be expressed in terms of theta, R and z.

\cos{\theta}=\frac{z-R\cos{\phi}}{r}

Then this becomes an intergral with a single variable phi with limits from zero to pi. So, using angles is straightforward.