ThomasMagnus
- 138
- 0
Coefficient of friction--Puck traveling up an incline
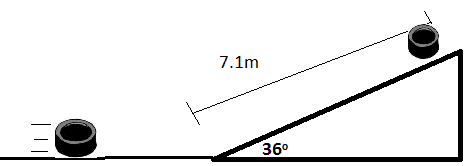
A hockey puck is moving at 13m/s when it starts climbing an incline. It travels 7.1m from the base of the incline before sliding back down the slope, as shown
Find the coefficient of friction between the puck and the incline.
First find acceleration of the puck
Vf=final velocity=0
Vo=initial velocity= 13m/s
d=distance=7.1
Vf2=Vo2+2ad
-169=14.2a, a=11.9m/s2
\SigmaFx=max
Since the puck is accelerating up the incline, the Force of Friction and the Force Parallel will be in the same direction.
FF+F||=max
FF=(\mu) FN
FN=mgcos(\theta)
F||=mgsin(\theta)
(\mu)mgcos(\theta) + mgsin(\theta)= 11.9m
m(\mugcos(36)+gsin36)=11.9m
Divide both sides by m, m cancels.
\mu=11.9/9.8cos36+9.8sin36
\mu=.87
The answer in the book is .77. Can you help me with where I am going wrong?
Thanks! =)
Homework Statement
A hockey puck is moving at 13m/s when it starts climbing an incline. It travels 7.1m from the base of the incline before sliding back down the slope, as shown
Find the coefficient of friction between the puck and the incline.
The Attempt at a Solution
First find acceleration of the puck
Vf=final velocity=0
Vo=initial velocity= 13m/s
d=distance=7.1
Vf2=Vo2+2ad
-169=14.2a, a=11.9m/s2
\SigmaFx=max
Since the puck is accelerating up the incline, the Force of Friction and the Force Parallel will be in the same direction.
FF+F||=max
FF=(\mu) FN
FN=mgcos(\theta)
F||=mgsin(\theta)
(\mu)mgcos(\theta) + mgsin(\theta)= 11.9m
m(\mugcos(36)+gsin36)=11.9m
Divide both sides by m, m cancels.
\mu=11.9/9.8cos36+9.8sin36
\mu=.87
The answer in the book is .77. Can you help me with where I am going wrong?
Thanks! =)
