Discussion Overview
The discussion revolves around designing a combinational circuit to multiply two 2-bit numbers, focusing on creating a truth table, K-maps, and the corresponding logic circuits for the outputs. The scope includes homework-related tasks and technical explanations of circuit design.
Discussion Character
- Homework-related
- Technical explanation
- Exploratory
Main Points Raised
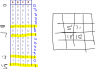
- One participant outlines the need for a truth table to represent the multiplication of two 2-bit numbers and questions how to start it.
- Another participant suggests filling out the truth table with the 2x2-bit inputs and resulting 4-bit output, and emphasizes the need for clarity in the truth table structure.
- A participant expresses confusion about forming expressions from the K-map and building the circuit from those expressions.
- There is a request for help in understanding how to derive the outputs from the K-map and how to construct the logic circuits for each output bit.
- Participants discuss the need to create separate circuits for each output bit (W, X, Y, Z) rather than combining them into one circuit.
- One participant asks about implementing a more complex expression and inquires about the number of OR gates required in the expression.
Areas of Agreement / Disagreement
Participants generally agree on the process of creating separate circuits for each output bit and the use of K-maps for logic design. However, there are varying levels of understanding regarding the formation of truth tables and expressions from K-maps, indicating some unresolved confusion.
Contextual Notes
Some participants express uncertainty about the correct structure of the truth table and the logic needed to derive outputs from the K-map. There are also mentions of specific circuit design techniques, but not all participants seem to fully grasp these concepts.