- #1
bonildo
- 14
- 1
Homework Statement
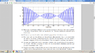
Hello, the plot in the image shows a modulated signal s(t), with one period of the modulating signal m(t). The mean value of m(t) is equal to zero . Its asked me to find the modulated index, the amplitude of the carrier, the equation of the message(m(t)) and the kind of modulation (DSB-SC or AM).
Homework Equations
s(t)=A*m(t)*cos*2*pi*fc*t) (dsb-sc modulation)
s(t)= (1+ka*m(t))*cos*2*pi*fc*t) (am modulation)
The Attempt at a Solution
I don't know, I'm really stuck in this exercise.