Comparing Currents: Two Wire Comparison Homework

[Winzer]

Homework Statement

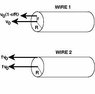
The diagram shows two wires; wire 1 and wire 2. The charge carriers in wire 1 (of circular cross section and radius R) have a drift speed down the wire that is not constant across the wire. Instead, the drift speed rises linearly from zero at the circumference (r=R) to at the center (r = 0), according to vd1(r)=Vo(1-(r/R)).The second wire (wire 2) has the same radius, the same density of charge carriers and a constant drift speed given by vd1(r)= fVo. Evaluate the ratio of the current carried by wire 2 to the current carried by wire 1, when f = 0.490.

Homework Equations

$$I=nqAV_{d}$$

$$\frac{qnAV_{d2}}{qnAV_{d1}}$$

The Attempt at a Solution

So since q,n,A are the same they cancel leaving:
$$\frac{I_{2}}{I_{1}}= \frac{V_{d2}}{V_{d1}}$$
I need to find vd now.

 

[fikus]

To find current in first wire you need to integrate. Sice speed is constant at fixed r you should write: $$dI=nqv(r)2\pi rdr$$ and then integrate.

Hope you understand why, else ask.

 

[Winzer]

got it thanks. Yes I know why