Potatochip911
- 317
- 3
Homework Statement
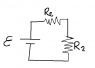
A real voltage source can be expressed as an ideal voltage source that is in series with a resistor that represents the inner resistance of the voltage source. This voltage source is a EMF and it is also in series with another resistor. Suppose both the EMF resistor ##R_\varepsilon## and the second resistor ##R_2## have complex impedance. Determine a) The current, b) the non-dc power that is dissipated in the second resistor and c) The requirements to achieve maximum dissipated power in the second resistor.https://physicsforums-bernhardtmediall.netdna-ssl.com/data/attachments/80/80085-d91a852075e6af6d2347539788417783.jpg
Homework Equations
##\tilde{v}=\tilde{i}z##
##z_ts=z_1+z_2+\cdots##
##z=|z|e^{j\phi}##
The Attempt at a Solution
For part a) the total impedance will be given by ##z_t=z_1+z_2=(R_\varepsilon +ja)+(R_2+jb)=(R_\varepsilon+R_2)+j(a+b)## so ##|z|=\sqrt{(R_\varepsilon+R_2)^2+(a+b)^2}## and ##\phi=tan^{-1}(\frac{a+b}{R_\varepsilon+R_2})## then from ##\tilde{i}=\frac{\tilde{v}}{z}##
$$\tilde{i}=\frac{ve^{-j\phi}}{\sqrt{(R_\varepsilon+R_2)^2+(a+b)^2}} \\
i=\frac{v\cos(\phi)}{\sqrt{(R_\varepsilon+R_2)^2+(a+b)^2}}
$$
now for b) would the non-dc power dissipated in the second resistor be ##P=i\Im{(R_2)}=ibj##?
Attachments
Last edited by a moderator: