- #1
james_1138
- 5
- 0
Hi, I am working on a simulation code that simulates the deformation of sand grains in 2D. The sand grains are modeled as simple polygons. However, during the simulation the grains can deform to create non-convex vertices. Further more, when deformation becomes extreme, there is a possibility that "self intersection" can occur (the polygon goes from being non-convex to complex).
My question is then, is there an algorithm that can determine which vertex has "self-penetrated" the polygon? Even if I check for intersections between all edges and determine that the polygon is now complex, I do not know which vertex has penetrated.
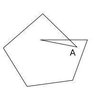
Here's an example where vertex A has "folded"
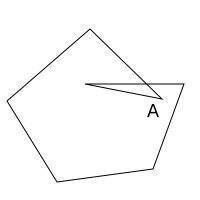
My question is then, is there an algorithm that can determine which vertex has "self-penetrated" the polygon? Even if I check for intersections between all edges and determine that the polygon is now complex, I do not know which vertex has penetrated.
Here's an example where vertex A has "folded"