- #1
Fisherlam
- 10
- 0
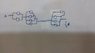
Hey there! I'm having some real trouble deciphering this complex resistor problem. I have heard of the Kirchhoff voltage and current rules and do know how to use them to solve some problems but I'm not sure how to apply them in this context, or if they are even used to solve this. As seen the the diagram, each block is a resistor with resistance of r, and I'm tasked to find out the net resistance across A and B, the answer given by the book is 2r. I would really appreciate some help in understanding how to solve them and perhaps a universal way to tackle such problems.
THANKS A LOT!
THANKS A LOT!