Complicated Definite Double Integral

[dBrandon/dC]

I've been working on a problem involving a large meteoroid passing over the Earth and what its gravitational effects would be on the Earth's mantle. I developed an equation for this, and I've worked it down to a certain point, but unfortunately, I'm not sure how to finally solve it. By the way, I downloaded a free trial version of Mathematica, but it doesn't seem to be able to solve the problem, either.

The equation is as follows:

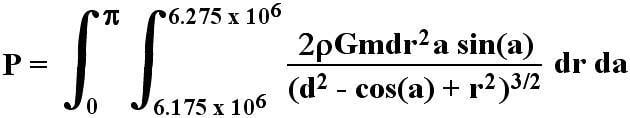
(I'm new here, so I didn't know the best way to input an equation.)
Any help that could be provided would be very much appreciated.

- Brandon

 

[LeonhardEuler]

The "r" part of the integral is doable. I get
$$P=\int_{0}^{\pi}2\rho Gmdr^{2}a\sin{a}\dot ( \ln{\sqrt{r^{2}+d^{2}-\cos{a}} +r} -\frac{r}{\sqrt{r^{2}+d^{2}-\cos{a}}})da\left|^{r=6.275*10^6}_{r=6.175*10^6}$$

Integrating the "a" part seems like it should be a nightmare, though. You could do a substitution u=-cos(a) if it wasn't for that a sitting outside. It's probably not expressible in elementary functions. Could you just evaluate it numerically?

 

[AlephZero]

Starting with the a integral,

$$\int \frac{a \sin a\, da}{(b^2 - \cos a)^{3/2}}$$

is an elliptic function of the 3rd kind according to http://integrals.wolfram.com.

My knowledge of elliptic functions doesn't extend to knowing if your definite integral equals something nice, but at least that's a start.