Precursor
- 219
- 0
Homework Statement
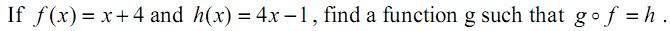
The attempt at a solution
g(f(x)) = h(x)
4f(x) + y = 4x - 1
4x + 16 + y = 4x - 1
y = -1 - 16
y = -17
so, g(x)= 4x + y = 4x - 17
Is this the correct way of going about this question? I used a guessing approach to this question. Is enough work shown to get full marks? Thanks.
The attempt at a solution
g(f(x)) = h(x)
4f(x) + y = 4x - 1
4x + 16 + y = 4x - 1
y = -1 - 16
y = -17
so, g(x)= 4x + y = 4x - 17
Is this the correct way of going about this question? I used a guessing approach to this question. Is enough work shown to get full marks? Thanks.