Computing the Legendre Symbol (2/p) for Odd Primes: A Proof and Explanation

[kingwinner]

"Let p be an odd prime, then we proved that the Legendre symbol

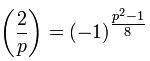
Note that this can be easily computed if p is reduced modulo 8.
For example, if p=59, then p≡3 (mod 8) and $$(-1)^{(p^2-1)/8}$$ = $$(-1)^{(3^2-1)/8}$$" (quote from my textbook)
====================================

Now I don't exactly see WHY p can be reduced modulo 8 without changing the answer.
Why can we be so sure that $$(59^2-1)/8$$ and $$(3^2-1)/8$$ will have the same parity? How can we prove this?

Thanks for explaining!

 

[Hurkyl]

Why can we be so sure that $$(59^2-1)/8$$ and $$(3^2-1)/8$$ will have the same parity? How can we prove this?

Isn't parity just another word for looking at the number modulo 2?

 

[kingwinner]

Yes, but my textbook says modulo 8 which I don't understand.

59≡3 (mod 2)
=> 59²≡3² (mod 2)
=> 59²-1 ≡ 3²-1 (mod 2)
But the trouble here is that there is no rule saying that I can multiply both sides by 1/8 (since 1/8 is not an integer)

 

[Hurkyl]

But the trouble here is that there is no rule saying that I can multiply both sides by 1/8 (since 1/8 is not an integer)

That's right. But, still, there is a rule that deals with division...

By the way, it's the parity of (p²-1)/8, not the parity of p, so maybe you should start with that?

 

[Hurkyl]

Or, I suppose, you could start with p=q mod 8 and work from there.

 

[kingwinner]

Sorry, I don't get it...

How should I begin?

 

[kingwinner]

I guess I should look at two cases...(p²-1)/8 is even and the other case (p²-1)/8 is odd.

(2/p)=1
<=> (p²-1)/8 is even
<=> (p²-1)/8 = 2k
<=> p²= 16k + 1
<=> p² ≡ 1 (mod 16)

<=> p ≡ ? (mod 8) <-----------this is the step I'm stuck...

Can someone help me, please?
Thank you!

 

[Hurkyl]

Can't you just try everything?

 

[kingwinner]

How? Can someone show me an example?

How do you go from mod 8 to mod 16??

 

[kingwinner]

To get the conrguence on the right hand side (i.e. precisely when (-1/p)=1), I will use the formula in the middle
(-1/p)=1 <=> (p-1)/2 is even <=> (p-1)/2 = 2k <=> p=1+4k <=> p≡1 (mod 4)

Following the same trick as above, to determine when (2/p)=1,
set $$[(p^2 -1)/8]$$ =2k
<=> $$p^2$$ = 16k +1
<=> $$p^2$$ ≡ 1 (mod 16)

<=> p ≡ ? (mod 8) <-----I'm stuck on this step. Can someone explain how to go from the previous step to this step?

Thanks for any help!

 

[kingwinner]

If we somehow already HAVE the answer on the right hand side, then it's easy to check that $$\frac{p^2-1}{8}$$ is odd for p = 3, 5 and it's even for p = 1, 7. But to do this, we actually need to know the correct answers in the first place.

But like in my textbook, it only proved the formula in the middle, without showing the conditions on the right, and I'm looking for a way to systematically derive the conditions on the right using the formula in the middle.

Also, why should the conditions be p≡ (mod 8)? Why not p≡ (mod 16)?? (as analogy, for (-1/p), the formula has 2 in the denominator of the exponent, and we get mod 4 on the right)
Having ONLY the formula in the middle, how to figure out what "modulus" to work with when we're trying to derive the conditions on the right?


Can someone explain this, please?
Thank you!

 

[Hurkyl]

Why not p≡ (mod 16)?
Do it for that then. What do you get?

 

[robert Ihnot]

We know p is an odd prime so there are only four cases which can be placed in two catagories: $$\pm1+8k; \pm3+8k$$ Of course, in some cases k could be even and represent things like 1+32k, etc.

In the first case, squaring, subtracting off 1, and dividing by 8: $$\frac{\pm16k +64k^2}{8}}$$

This gives an even result which goes for 8k+1 and 8k +7. The second situation is negative.

The factor 8 is introduced by use of a way to get the result. It comes from the sum formula for a product series of powers of -1: 1+2++++(p-1)/2 =(p-1)/2*(p+1)/2*1/2 =(p^2-1)/8. http://www.mathreference.com/num-mod,qr12.html

_In that case we arrive at 2^(p-1)/2 = (-1)^(p^2-1)/8. Since 2^(p-1)/2 can be only +/1, and all squares are +1--which is half the cases, we have our result.