Conceptual capacitor/inductor problem

[Learnphysics]

Hi guys,

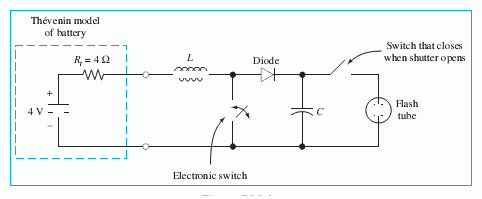
This is a basic circuit that you'd commonly see in a flash Camera.
Hambley says (roughly paraphrased):

When the electronic switch is toggled rapidly (1000s of times a second) the inductor charges due to a change in current. v=L(di/dt).

The diode allows current to flow into the capacitor to create a build up of electrons on one of it's plates creating a growing voltage cross the capacitor. Once it reaches 100s of volts on the positive plate of the capacitor, The Shutter switch closes discharging the capacitor into the flash tube.

Fair enough.

But I have some questions:

Firstly, Why do we even need an inductor? What if we were to simply attach the battery (DC voltage) to a capacitor (in parralell) and let it charge to 100V. I understand this is dependent on the size of the capacitor by: v= 1/C(integral(idt)).

(Speaking of which, and not to get too distracted but, the above formula seems to suggest that voltage across a capacitor is inversely proportional to it's capacitance...Why is this the case I'd figure that the voltage across a capacitor would only INCREASE if we had large capacitors.)
I know I'm probably missing something fundamental when asking this question.

 

[gneill]

The battery is just 4V. The flash bulb requires hundreds of volts to trigger. How many 1.5V AAA cells would you need in series to drive a flashbulb?

The inductor has a property that, for current, acts like inertia for mass; Once you establish a current through it, it doesn't want to change quickly. In fact, if you interrupt the path of the current suddenly, using the energy stored in the magnetic field the inductor will 'generate' any voltage necessary to maintain that current. If this means arcing across the switch contacts, so be it! If an alternate path for the current is available that doesn't required such extreme voltages, it will take it...

In the given circuit, the alternative path is driving the current through the diode and into the capacitor. Each time the "Electronic switch" opens, the inductor drives current into the capacitor, increasing the charge on the capacitor and so increasing the voltage across the capacitor. Thus the voltage established across the capacitor can be many times greater than the supply battery voltage. There are physical limits to the process determined by the values of the circuit components and the switching rate of the "Electronic switch", but that's not essential to understanding the underlying principle.

The voltage across a capacitor depends upon the capacitance and the charge stored. The unit of capacitance, the Farad, is equivalent to Coulombs per Volt, so V = Q/C. The voltage on the capacitor of a given size depends upon the amount of charge impressed upon the capacitor. A smaller capacitor will result in a larger voltage for a given amount of charge. HOWEVER! The brightness and duration of the flash will depend upon how much ENERGY is delivered to the bulb when it triggers. The energy stored in the capacitor depends on both the voltage and the sze of the capacitor: E = (1/2)CV².

 

[CWatters]

Firstly, Why do we even need an inductor? What if we were to simply attach the battery (DC voltage) to a capacitor (in parralell) and let it charge to 100V. .

It wouldn't charge to 100V. It would only charge to the battery voltage 4V.

Suppose you started with a capacitor charged to 6V and connected it in parallel with a 4V battery. Which way would the current flow?