Condition for stable equlibrium

[RajarshiB91]

Homework Statement

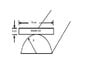
A homogeneous wooden bar of length 10 cm, thickness 4 cm and weight 1 Kg is balanced
on the top of a semicircular cylinder of radius R as shown below. Calculate the
minimum radius of the semicircular cylinder if the wooden bar is at stable equilibrium.

Homework Equations

Potential energy E=mgh and its derivatives.

The Attempt at a Solution

Stable equilibrium means the first derivative of potential energy is zero and its second derivative must be greater than zero(local minima). So, I have to express the PE of the wooden bar in terms of R and find minimum R to satisfy above conditions. But here the CM of the bar is at R+(4/2)=R+2 cm above the ground. So, second derivative of PE is always 0? Where am I going wrong? Also, how to approach problems like these in general? I had read about equilibrium a long time back and the concepts are a bit muddled up.

 

[BvU]

The CM doesn't stay at R+2 if the beam is wiggled !

 

[RajarshiB91]

The CM doesn't stay at R+2 if the beam is wiggled !

Thanks BvU. Yes, I googled similar problems and understood what needs to be done. By displacing the block by θ I calculate the new CM height which comes out to be
h=Rcosθ+Rθsinθ+2cosθ
Now, it is just differentiating twice. So, for equilibrium, is the width of the block(10 cm) irrelevant? I didn't find it's use in the height equation or am I missing something?

 

[BvU]

Ah, you mean the length !

Didn't work out h myself, and you don't show the steps, so I can't really tell. Suppose you're right.