A Conductivity and Integration over Fermi-Sphere?

[Abigale]

Hi,
I am reading "An Introduction of Solid State Physics" from Ibach Lüth and don't understand the integration process.
They write $$\sigma=\frac{e^2}{8\pi^3 \hbar}
\int df_{E}dE \frac{v^2_x(\bf{k})}{v(\bf{k})} \tau(\bf{k}) \delta(E-E_F)
$$

$$
= \int_{E=E_F}^{}df_{E} \frac{v^2_x(\bf{k})}{v(\bf{k})} \tau(\bf{k})
$$

But why does $k$ NOT become $k_F$ after the Integration of the Delta-function?

I would think that the integral becomes immedately after the dE-integration:
$$
= \int_{E=E_F}^{}df_{E} \frac{v^2_x(\bf{k_F})}{v(\bf{k_F})} \tau(\bf{k_F})
$$

THX
Abbi

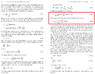
I also add the pages

 

[DrDu]

Yes, you are right, but this is only a matter of notation. k is still a vector and will have different length for different directions as long as the Fermi surface is not spherical.

 

[Abigale]

I don't understand the notation $dS_E$.
$$d\bf{k} = k^2 sin\theta d\theta d\phi dk$$
$$ = dS_k dk_\bot $$ This means a surface-element times a radial distance-element perpendicular to the surface-element. Both in k-space.

In the book instead of $dS_k$ the expression $dS_E$ is used. They say $dS_k= dS_E dk_\bot$

What means exactly $dS_E$?
If I think at the notation $$ dS_k= k^2 sin\theta d\theta d\phi$$,
it should be $$dS_E=E({\bf k})^2 sin\theta d\theta d\phi$$

But then the units don't correspond anymore to k-space:
$$d{\bf k} =dS_E dk_\bot$$ which corresponds to $$ \frac{1}{m^3}=\frac{eV}{1}\frac{1}{m}$$