- #1
yungman
- 5,755
- 292
I want to verify my understanding about skin effect and plane wave of conductor wire.
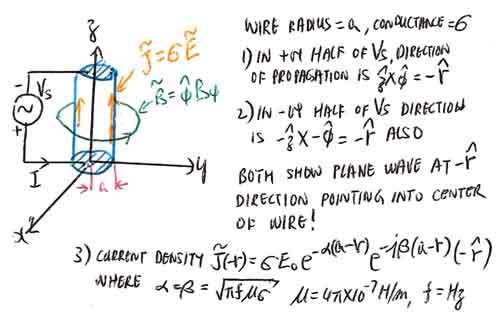
In the diagram, assume long straight on z axis. Wire with radius = a and conductance = [itex] \sigma [/itex]. Accouding to the equation shown, the plane wave is going towards the center of the wire only regardless of the instantaneous polarity of the Vs. My questions are:
1) Is this how to look at the skin depth? By putting a voltage across the wire that generate the current density [itex] \tilde J = \sigma \tilde E[/itex] in say +ve z direction according to the drawing. As noted, [itex] \tilde B = \hat \phi B_{\phi}[/itex]. The direction of propagation is [itex] \hat z X \hat {\phi} = -\hat r [/itex]. Are my drawing and description correct?
2) You can see in both polarity of Vs, the propagation is towards the center of the wire. But we know there is a plane wave propagate out of the wire into the space and is perpendicular to the wire in [itex] \hat r [/itex] direction. How come I don't see it in the equation?
3) This is the most confusing question. Why is the E field started at the surface and propagate into the wire. When you apply voltage across the wire, the E at the center of the wire should be the same as right underneath the surface of the wire. You can look at it as the E start at the center and decay when traveling outward since the voltage across the wire is same at the center of the wire as right below the surface.
In another words, why we start considering the E on the surface only and calculate the plane wave instead of starting at the center of the wire and calculate outwards. What make the E on the surface only? From the book, it is almost like they start the E right above the surface of the wire in the space, and then use boundary condition that tangential E = [itex] \hat z E_0[/itex] is continuous cross the boundary so the E right below the surface of the wire is the same E = [itex] \hat z E_0[/itex]!
In the diagram, assume long straight on z axis. Wire with radius = a and conductance = [itex] \sigma [/itex]. Accouding to the equation shown, the plane wave is going towards the center of the wire only regardless of the instantaneous polarity of the Vs. My questions are:
1) Is this how to look at the skin depth? By putting a voltage across the wire that generate the current density [itex] \tilde J = \sigma \tilde E[/itex] in say +ve z direction according to the drawing. As noted, [itex] \tilde B = \hat \phi B_{\phi}[/itex]. The direction of propagation is [itex] \hat z X \hat {\phi} = -\hat r [/itex]. Are my drawing and description correct?
2) You can see in both polarity of Vs, the propagation is towards the center of the wire. But we know there is a plane wave propagate out of the wire into the space and is perpendicular to the wire in [itex] \hat r [/itex] direction. How come I don't see it in the equation?
3) This is the most confusing question. Why is the E field started at the surface and propagate into the wire. When you apply voltage across the wire, the E at the center of the wire should be the same as right underneath the surface of the wire. You can look at it as the E start at the center and decay when traveling outward since the voltage across the wire is same at the center of the wire as right below the surface.
In another words, why we start considering the E on the surface only and calculate the plane wave instead of starting at the center of the wire and calculate outwards. What make the E on the surface only? From the book, it is almost like they start the E right above the surface of the wire in the space, and then use boundary condition that tangential E = [itex] \hat z E_0[/itex] is continuous cross the boundary so the E right below the surface of the wire is the same E = [itex] \hat z E_0[/itex]!