hgfhh123
- 4
- 0
Homework Statement
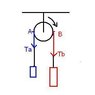
I am a little confused about the concept of tension as it relates to pulleys. I am studying torque right now, and it says in the textbook that the tension in the rope around a pulley produces a torque that causes the pulley to turn. I don't fully understand this. I thought that tension was a pair of opposing forces that acted throughout the rope at each point in the rope. However, I don't understand how the same force would cause the pulley to turn. Since there is no friction between the rope and pulley, I don't understand why the pulley would turn in the first place.