Forces on two different blocks with two pulleys

[Amphibia]

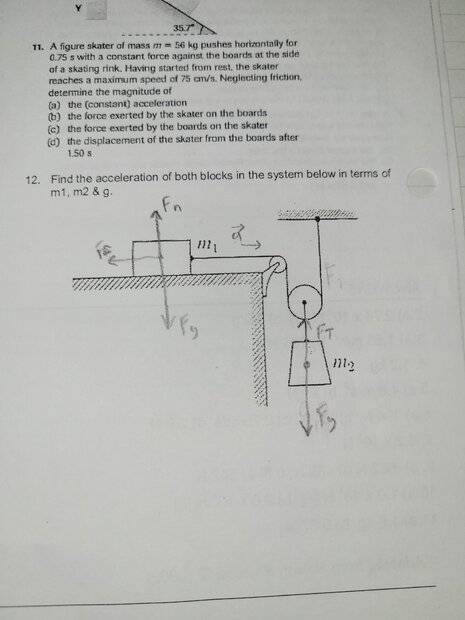
Homework Statement

Question 12

Relevant Equations

Scalar equations

I don't know what to do as I know the forces acting on it but not the scalar like I just don't understand the question with two different pulleys I know the tension same everywhere

 

[Lnewqban]

Welcome!
How would you apply what you have studied about forces and masses and accelerations to this problem?
Don't let those pulleys confuse you.

 

[Amphibia]

Welcome!
How would you apply what you have studied about forces and masses and accelerations to this problem?
Don't let those pulleys confuse you.

Well the forces in fnetx and fnety the m1 fnety is 0 so there's fnetx and Ft-Ff for the m1 fnetx and m2 has fnetx=0 and the Fnety is Ft-Fg my only known is gravity

 

[Lnewqban]

Well the forces in fnetx and fnety the m1 fnety is 0 so there's fnetx and Ft-Ff for the m1 fnetx and m2 has fnetx=0 and the Fnety is Ft-Fg my only known is gravity

If all Fnet's are zero, there is no movement or acceleration.
But the wording of the problem suggests that there is certain acceleration, and nothing is told about coefficient of friction.

 

[Amphibia]

If all Fnet's are zero, there is no movement or acceleration.
But the wording of the problem suggests that there is certain acceleration, and nothing is told about coefficient of friction.

Oh so there's no friction the objects are stationary and m1 and m2 are the same masses or I think m1 is = to more than the tension

 

[Lnewqban]

Nothing suggests that m1 and m2 are the same masses.
I believe that you can assume that there is no friction force between m1 and the flat surface, that the string is non-extensible and that the pulleys are massless and free of friction at their pivots.

Then, the weight of m2 is not balanced by any other force and it should induce acceleration of the whole system (m1 and m2).

However, m1 and m2 can't move at the same velocity, and that should be considered and the forces acting on each should be analyzed by free-body diagrams of each mass.

 

[Amphibia]

Nothing suggests that m1 and m2 are the same masses.
I believe that you can assume that there is no friction force between m1 and the flat surface, that the string is non-extensible and that the pulleys are massless and free of friction at their pivots.

Then, the weight of m2 is not balanced by any other force and it should induce acceleration of the whole system (m1 and m2).

However, m1 and m2 can't move at the same velocity, and that should be considered and the forces acting on each should be analyzed by free-body diagrams of each mass.

Ok so what I see now is that they don't have the same acceleration, the rope is a constant that doesn't extend, velocity is different, the masses are different and that I only see related are the normal force and the tension force of each other

 

[haruspex]

they don't have the same acceleration

Right, but what is the relationship between the two accelerations?

 

[Amphibia]

Right, but what is the relationship between the two accelerations?

That both of their fnet are the same or they have the same amount of forces on each other

 

[Orodruin]

That both of their fnet are the same or they have the same amount of forces on each other

No. The forces on the objects are not related in any such way.

Rather than guessing, start by drawing the free body diagrams for each mass. Then ask yourself what information you get out of that and what information you get from the string being inextensible.

 

[haruspex]

That both of their fnet are the same or they have the same amount of forces on each other

The relationship is kinematic, nothing to do with forces.