- #1
ARoyC
- 56
- 11
Hi. I am not being able to understand how we are getting the following spectral decomposition. It would be great if someone can explain it to me. Thank you in advance.
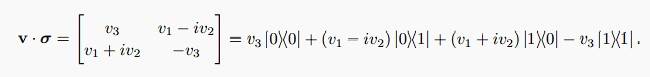
Oh! Then we can go to the LHS of the equation from the RHS. Can't we do the reverse?vanhees71 said:It's simply a non-sensical equation. On the one side you write down a matrix, depicting matrix elements of an operator and on the other the operator itself. Correct is
$$\hat{A}=v_3 |0 \rangle \langle 0| + (v_1-\mathrm{i} v_2) |0 \rangle \langle 1| + (v_1+\mathrm{i} v_2) |1 \rangle \langle 0| - v_3 |1 \rangle \langle 1|.$$
The matrix elements in your matrix are then taken with respect to the basis ##(|0 \rangle,|1 \rangle)##.
$$(A_{jk})=\langle j|\hat{A}|k \rangle, \quad j,k \in \{0,1 \}.$$
To see this, simply use ##\langle j|k \rangle=\delta_{jk}##. Then you get, e.g.,
$$A_{01}=\langle 0|\hat{A}|1 \rangle=v_1-\mathrm{i} v_2.$$
How are we getting the very first equality that is A = Σ|j><j|A|k><k| ?vanhees71 said:Sure:
$$\hat{A}=\sum_{j,k} |j \rangle \langle j|\hat{A}|k \rangle \langle k| = \sum_{jk} A_{jk} |j \rangle \langle k|.$$
The mapping from operators to matrix elements with respect to a complete orthonormal system is one-to-one. As very many formal manipulations in QT, it's just using the completeness relation,
$$\sum_j |j \rangle \langle j|=\hat{1}.$$
Oh, okay, thanks a lot!Haborix said:$$\hat{A}=\hat{1}\hat{A}\hat{1}=\left(\sum_{j} |j \rangle \langle j|\right)\hat{A}\left(\sum_{k} |k \rangle \langle k|\right)=\sum_{j,k} |j \rangle \langle j|\hat{A}|k \rangle \langle k| = \sum_{jk} A_{jk} |j \rangle \langle k|.$$
Spectral decomposition is a mathematical process used to break down a complex signal or data set into simpler components, known as spectral components. These components can be analyzed separately to better understand the original signal or data set.
Spectral decomposition is commonly used in various fields of science, including physics, chemistry, and geology. It is used to analyze complex signals such as sound waves, electromagnetic waves, and seismic waves, as well as data sets from experiments or observations.
Spectral decomposition and Fourier analysis are closely related, but there are some key differences. While both methods break down a signal into simpler components, spectral decomposition uses a wider range of mathematical techniques and can handle more complex signals. Additionally, spectral decomposition can be used on non-periodic signals, whereas Fourier analysis is limited to periodic signals.
Yes, spectral decomposition can be applied to image processing. It is commonly used in image compression techniques, where the image is broken down into spectral components and then compressed for storage or transmission. Spectral decomposition can also be used for image enhancement and feature extraction.
While spectral decomposition is a powerful tool, it does have some limitations. It may not be suitable for highly nonlinear signals, and the results can be affected by noise or measurement errors. Additionally, the interpretation of the spectral components may be challenging, especially for complex signals.