- #1
Hereformore
- 61
- 0
So a standing wave is one which looks to be standing still at certain harmonic frequencies. At these frequencies, when the wave reflects off the end, it will undergo a phase change of 180 degrees. This creates constructive interference as shown below:
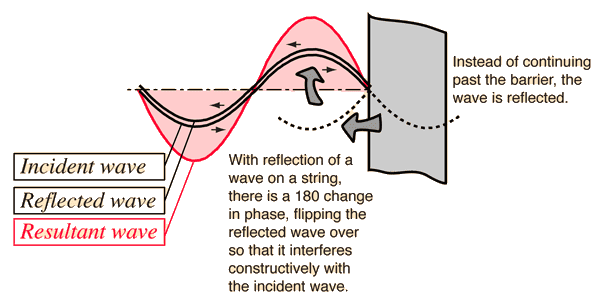
In the case of a wave on a string, since that would constitute a transverse wave, when the wave hits a barrier, much like with thin film interference, the reflected wave is shifted by 180 degrees.
in the case of a longitudinal wave, such as with an open-closed or open open air pressure system, the phase change occurs at the open end(s) but not at the closed ends.
What I don't understand is, if the reflected wave is constructive, and in phase with the incident wave, then why are standing wave diagrams always drawn with the reflected wave out of phase/having destructive interference? Am i misinterpreting the diagrams?
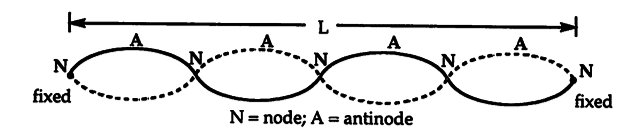
See below for standing waves:
See below for Longitudinal waves:
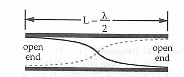 (Open Open = phase change at both ends)
(Open Open = phase change at both ends)
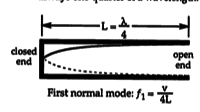 Open Closed = Phase change only at open end.
Open Closed = Phase change only at open end.
Also otherwise, is my understanding of what's going on (with the reflections and phase changes) accurate? Thanks guys!
In the case of a wave on a string, since that would constitute a transverse wave, when the wave hits a barrier, much like with thin film interference, the reflected wave is shifted by 180 degrees.
in the case of a longitudinal wave, such as with an open-closed or open open air pressure system, the phase change occurs at the open end(s) but not at the closed ends.
What I don't understand is, if the reflected wave is constructive, and in phase with the incident wave, then why are standing wave diagrams always drawn with the reflected wave out of phase/having destructive interference? Am i misinterpreting the diagrams?
See below for standing waves:
See below for Longitudinal waves:
Also otherwise, is my understanding of what's going on (with the reflections and phase changes) accurate? Thanks guys!