Hi tiny-tim,
tiny-tim said:
i think i disagree with this …
And I am sorry, but I disagree with you.

tiny-tim said:
the capacitors clearly
can be described as connected in series, but they
can't be described together as a
single capacitor, at least not one that obeys the usual rules …
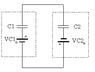
usually, when we connect two capacitors in series, the charge on each is the same, and so the charge on each side of the-pair is the same, and so the-pair can be considered a single capacitor
but the-pair in this case has
unequal charges on its two (outer) plates

There are no outer plates, as both pairs of plates are connected: The positive plate of one capacitor to the negative plate of the other one, and the negative plate to the positive plate of the other capacitor. As the positive and negative charges have a metallic contact to move from one plate to the other, they will partially neutralise each other on both plates, till the voltage becomes equal on both capacitors.
I stick to my statement that the distinction between series and parallel has no sense if two circuit elements (two-poles) are connected only to each other.
Two elements are connected in series if they have a common pair of terminals and nothing else is connected to that junction. The free terminals are connected to the circuit.
Two elements are connected in parallel if both their terminals are common with the other element. The pairs of common terminals are connected to the circuit.
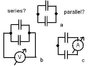
See drawing a. Two capacitors are connected to each other. They have a pair of terminals connected, and nothing else is connected to the junction, so the capacitors are connected in series.
But the other terminals are also connected, so they have two pairs of terminals in common, so they are parallel. So WHICH one?
If you add a third element, an ideal voltmeter or an ideal ammeter, which does not change anything, the situation becomes clear. b is parallel connection. C is series connection. And the charges and voltage of the individual capacitors are the same in both cases.
If Q1 was the charge on capacitor C1 and Q2 was the charge on C2, and Q1>Q2, after connecting the capacitors, the charges rearrange so the voltage is the same on both capacitors. The connected plates both will be either positively or negatively charged. There will be q1 charge on C1 and q2 charge on C2, and the common voltage is V=q1/C1=q2/C2. As the charge is conserved, Q1-Q2=q1+q2.
There are two equation for the unknown charges q1 and q2:
q1+q2=Q1-Q2
q1/C1=q2/C2.
It is easy to solve, and then V=(Q1-Q2)/(C1+C2) just like in case of parallel capacitors!.
ehild