jonhswon
- 10
- 4
Hello,
As far I know, in a closed system both, linear and angular monentums, are conserved.
İmagine such a scenario: everything is motionless, both momentums zero initially, then from a disk are fired (compressed spring push) two equal mass balls at same speed but opposite direction. Now balls fly away and disk is spinning. Linear momentum after firing is still zero, but angular momentum is not? What is happening?
(All usual assumptions in place, inertial reference, massless springs, etc..)
Thnaks in advance.
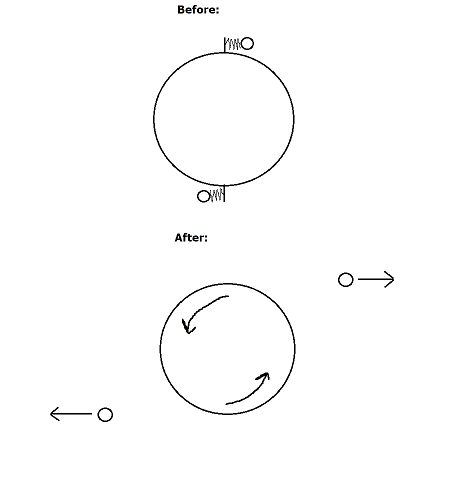
As far I know, in a closed system both, linear and angular monentums, are conserved.
İmagine such a scenario: everything is motionless, both momentums zero initially, then from a disk are fired (compressed spring push) two equal mass balls at same speed but opposite direction. Now balls fly away and disk is spinning. Linear momentum after firing is still zero, but angular momentum is not? What is happening?
(All usual assumptions in place, inertial reference, massless springs, etc..)
Thnaks in advance.
Last edited: