RavenBlackwolf
- 15
- 0
Homework Statement
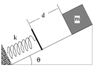
A 4.0 kg block starts at rest and slides a distance d down a frictionless 35.0
a) What is the value of d?
b) What is the distance between the point of first contact and the point where the block's speed is greatest?
Homework Equations
Ui+Ki=Uf+Kf
US=1/2kx2
UG=mgh
K=1/2mv2
The Attempt at a Solution
a) This one I got
1/2kx^2=mgΔh
1/2(429)(.162)=mgΔh
Δh=.244
d=.244-.16=.084m (correct answer)
b) This one I'm not sure of
1/2mv2+mgh=1/2mvf2+mg((.16-x)sin(35))+1/2kx2
I got that the velocity at contact is .972 m/s but how do I get the final velocity value? I need it to use the conservation of energy law the way I set it up. I've found similar questions to this online but none of them provide actual explanations/calculations for this part. I'm aware that it accelerates still once it hits the spring but then what?
Attachments
Last edited by a moderator: