Conservation of mechanical energy

[Anonymous123451234]

Derive equation v= √((2gh)/(1+.5(m/M)(r/R)^2)) by applying conservation of mechanical energy.

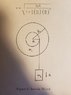
A string is attached to a hanging mass and wrapped around a small cylinder. The hanging mass is released from rest from an initial height (h) and accelerates to the floor. The theoretical velocity (v) of the hanging mass just before it strikes the floor can be determined by applying conservation of mechanical energy to the system.

v =velocity
m =hanging mass
M =mass of wheel
r =radius of wheel
R =radius of small cylinder
h =height

Ei=Ef
KEi+PEi = KEf+PEf
mgh = .5mv^2 + .5Iw^2
mgh = .5mv^2 + .5(.5Mr^2)(v/R)^2
2mgh = mv^2 + (M/2)(r^2/R^2)v^2
2mgh = (m + (M/2)(r^2/R^2)) v^2
√((2mgh)/(m + (M/2)(r^2/R^2))) = vWhat am I doing wrong?

 

[DoItForYourself]

Hello,

Firstly, please describe the problem in more detail. What do m, M, r, R and h stand for? In which situation you apply the conservation of mechanical energy?

1) You can divide both the numerator and the denominator (of the square root) by m.

2) Check if m and M are used correctly (seems like M is m and m is M).

 

[Anonymous123451234]

Hello,

Firstly, please describe the problem in more detail. What do m, M, r, R and h stand for? In which situation you apply the conservation of mechanical energy?

1) You can divide both the numerator and the denominator (of the square root) by m.

2) Check if m and M are used correctly (seems like M is m and m is M).

I updated the post with more info but I think it's irrelevant.
The conservation of mechanical energy is KEi+PEi=KEf+PEf
KEi and PEf both equal 0
So I'm starting with the equation PEi = KEf or mgh = .5mv^2 + .5Iw^2

And I need to show work to rearrange it to v= √((2gh)/(1+.5(m/M)(r/R)^2))

I made a lower case m & r, and a capital M & R to show that they are different variables as I cannot to subscript on my computer.

 

[DoItForYourself]

Nice, this makes more sense. But I still have some questions:

1) Is the small cylinder initially in the same level with the hanging mass (h)?
2) The problem does not refer to a wheel. Is the wheel attached to the small cylinder? Or the wheel is the small cylinder?

I think that a sketch would help in this situation.

 

[haruspex]

Is the small cylinder initially in the same level with the hanging mass (h)?

I cannot see that that matters. The mass descends by h, the wheel and cylinder do not.

The problem does not refer to a wheel. Is the wheel attached to the small cylinder? Or the wheel is the small cylinder?

I deduce that the cylinder is considered massless but is attached coaxially to a wheel.
Two things strike me as wrong, though.
1. The wheel is not described as a uniform disc, so I would have thought the moment of inertia was more like that of a ring, Mr² (or MR² - see 2 below).
2. Someone is confused between r and R. I suspect that these have been crossed over in the definitions. As it stands, the equation to be proved is wrong, and the attempt by anon is right (except for point 1).

 

[DoItForYourself]

I cannot see that that matters. The mass descends by h, the wheel and cylinder do not.

I deduce that the cylinder is considered massless but is attached coaxially to a wheel.
Two things strike me as wrong, though.
1. The wheel is not described as a uniform disc, so I would have thought the moment of inertia was more like that of a ring, Mr² (or MR² - see 2 below).
2. Someone is confused between r and R. I suspect that these have been crossed over in the definitions. As it stands, the equation to be proved is wrong, and the attempt by anon is right (except for point 1).

Yes, this is absolutely right. The potential energy of wheel and cylinder will not be changed anyway.

I agree with the assumption that the small cylinder is massless.

1) If the wheel is a ring, does it have to be uniform in order for the moment of inertia to be Μr²?

2) If the wheel is a uniform disc, the equation to be proved is wrong only in terms of m and M (the ratio must be M/m). Right?

 

[Anonymous123451234]

Nice, this makes more sense. But I still have some questions:

1) Is the small cylinder initially in the same level with the hanging mass (h)?
2) The problem does not refer to a wheel. Is the wheel attached to the small cylinder? Or the wheel is the small cylinder?

I think that a sketch would help in this situation.

Here's a diagram

 

[Anonymous123451234]

Figured it out , thanks for taking your time to help me!

 

[haruspex]

Yes, this is absolutely right. The potential energy of wheel and cylinder will not be changed anyway.

I agree with the assumption that the small cylinder is massless.

1) If the wheel is a ring, does it have to be uniform in order for the moment of inertia to be Μr²?

2) If the wheel is a uniform disc, the equation to be proved is wrong only in terms of m and M (the ratio must be M/m). Right?

Yes.