Conservation of Momentum initial velocity curved path

[pconn5]

Homework Statement

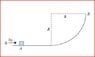
The frictionless track is made of a straight horizontal section and a quarter-circle with radius R = 5 m. A 1 Kg lump of putty is thrown toward the stationary 4 Kg block, and the block starts to slide with the putty stuck on it after the collision. If the normal force acting on the block/putty from the track is 98 N at point B, find the initial speed v0 of the putty.

Homework Equations

m1v0=(m1+m2)(vf)
...energy equation?

The Attempt at a Solution

I have been trying to use the energy equation to solve this problem but I am getting nowhere. The answer is 70 m/s. I can't seem to figure out what the velocity would be at the bottom of the arc. According to a(norm)=v^2/R, I found that v=9.8995 but don't know what to do with that...

 

[rock.freak667]

Well depending on where B is the velocity would be different.

But say B is just at the bottom of the arc, then on the arc the forces acting are the Normal force R and the weight W. The resultant of these two gives mv^2/r

\frac{mv^2}{r}=R-W

so find v from that.

Then put that into the momentum equation.

 

[pconn5]

Ok I got it now. Thanks for the help.