Tanya Sharma
- 1,541
- 135
Homework Statement
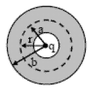
The region between two concentric spheres of radii a and b(>a) contains volume charge density ρ(r) = C / r where C is a constant and r is the radial distance, as shown in figure. A point charge q is placed at the origin, r= 0. Find the value of C for which the electric field in the region between the spheres is constant (i.e., r independent).
A) q/πa2
B) q/π(a2+b2)
C) q/2πa2
D) q/2πb2
Homework Equations
ε∫E.dS = qfree
The Attempt at a Solution
Let us consider a a gaussian surface, a concentric sphere at radius r .
Applying Gauss law
ε∫E.dS = q + 4πC(r2-a2)
εE(4πr2) = q + 4πC(r2-a2)
E = q/(4πr2ε) + C(r2-a2)/(εr2)
Now for E to be constant ,
q-4πca2 = 0 or C=q/(4πa2) .This is not given as one of the options .
I would be grateful if somebody could help me with the problem.