fib1123
Moved from a technical forum, so homework template missing.
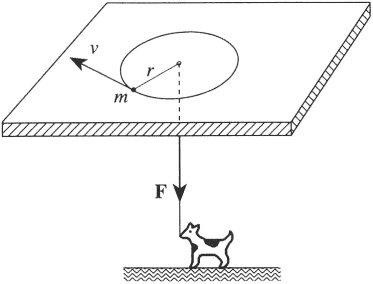
A mass m is attached at the end of the string. The mass moves on a frictionless table, and the string passes through a hole in the table, under which someone is pulling on the string to make it taut at all times. Initially , the mass moves in a circle, with kinetic energy [E][/0] . The string is slowly pulled, until the radius of the circle is halved. How much work is done?
I calculated the work and the result is
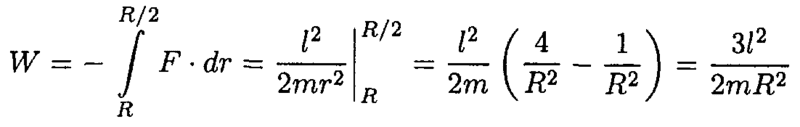
but my question is: Why is the rotational kinetic energy constant during the motion?
I calculated the work and the result is
but my question is: Why is the rotational kinetic energy constant during the motion?
Attachments
Last edited by a moderator: