Viraam
- 66
- 2
Homework Statement
Homework Equations
## v = r \omega##
The Attempt at a Solution
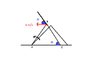
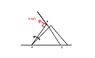
Velocity of point B= ##v_B = 4 \times \omega = 4 ## m/s
Since the separation between B and C is constrained to be a constant, Velocity of B along rod = Velocity of C along the rod
## \Rightarrow v_B \cos \theta = v_C \cos \theta ##
## v_B = v_C = 4 ##m/s
However the answer provided is ## v_C = 4 \sqrt 3 ## m/s. Where did I go wrong?