sami23
- 69
- 1
Homework Statement
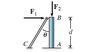
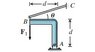
Which of these bodies has redundant constraints for the given loading conditions? F_1 and F_2 are applied, known forces. In the first choice, the support at A is fixed and a cable connects points B and C. In the second choice, the support at A is a smooth pin, and a cable connects points B and C. In the third choice, the support at A is a single thrust bearing, and a cable connects points B and C.
Check all that apply.
Homework Equations
Redundant constraints - when a body has more supports than necessary to hold it in equilibrium it becomes statically indeterminate.
The Attempt at a Solution
the first and last seem to have redundant constraints.