- #1
marcom
- 17
- 5
Hi,
Could you please help me understand the following example from page 76 of "QFT for the gifted amatur"?
I can't see how the following integral
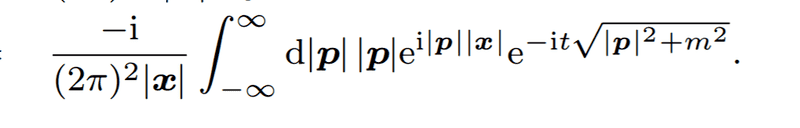 becomes
becomes
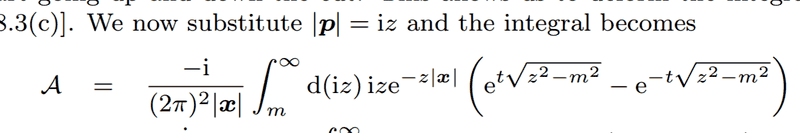
Thanks a lot
Could you please help me understand the following example from page 76 of "QFT for the gifted amatur"?
I can't see how the following integral
Thanks a lot