Joshua Pham
- 14
- 0
Homework posted in wrong forum, so no template
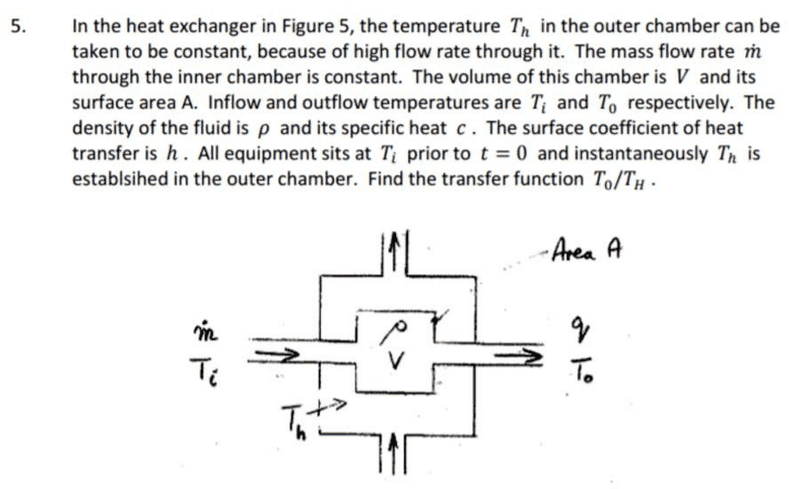
Hello guys, in the question attached, my understanding is that there is a heat transfer
 that heats the fluid from an initial
that heats the fluid from an initial
 at the input, to
at the input, to
 at the output. This heat transfer is via convection from walls of temperature
at the output. This heat transfer is via convection from walls of temperature
 .
.
Firstly,
 .
.
Because the walls are
 and the fluid is of a lower temperature, this heat transfer is via convection from the walls. The correct answer says that
and the fluid is of a lower temperature, this heat transfer is via convection from the walls. The correct answer says that
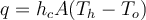 . Why is this? Why not
. Why is this? Why not
 ? or
? or
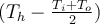 . The fluid next to the wall is heated and changes until it reaches
. The fluid next to the wall is heated and changes until it reaches
 at the outlet, so how do we know which temperature to use in the convection equation where heat is being transferred from the walls to the fluid?
at the outlet, so how do we know which temperature to use in the convection equation where heat is being transferred from the walls to the fluid?
Firstly,
Because the walls are