smart_worker
- 131
- 1
B]1. Homework Statement [/B]
Find whether the series is convergent or divergent
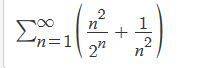
By ratio test I have,
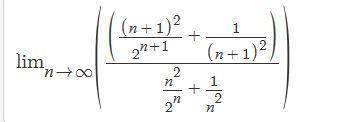
I would apply L'Hôpital's rule to find the value of limit but before that how do i simplify the expression? It has fractional part both in the numerator as well as in the denominator.
Find whether the series is convergent or divergent
Homework Equations
The Attempt at a Solution
By ratio test I have,
I would apply L'Hôpital's rule to find the value of limit but before that how do i simplify the expression? It has fractional part both in the numerator as well as in the denominator.
Last edited: