Conversions between intrinsic/extrinsic coordinates

[Jhenrique]

I noticed that in wiki there is the follows conversion:

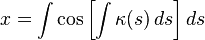
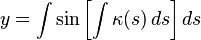
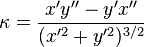
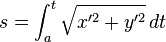
that is the conversion beetwen the cartesian coordinates and the intrinsic (arc length, curvature) "coordinate". In this case, the system is 2D.


There is the 3D case too:

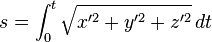
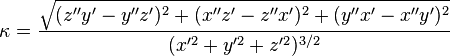
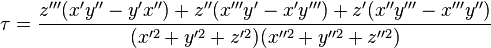
However, is missing the (x, y, z) coordinates in terms of (s, κ, τ). Where I can find this conversion?

 

[jvicens]

Hello,

Thank you for bringing this up. The conversion between Cartesian coordinates and intrinsic coordinates can be found in many textbooks and online resources. In the 3D case, the conversion can be written as:

x = s cos(τ)cos(κ)
y = s sin(τ)cos(κ)
z = s sin(κ)

Where s is the arc length, κ is the curvature, and τ is the torsion. This conversion is derived from the Frenet-Serret formulas, which describe the relationship between the tangent, normal, and binormal vectors of a curve in 3D space.

I hope this helps and please let me know if you have any further questions.