Convert to Center of Mass Reference Frame

[rdemyan]

Homework Statement

Convert a lab frame diagram to center of mass reference frame

Relevant Equations

See post

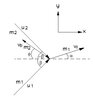
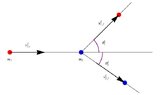
I'm trying to convert the first attached diagram to the center of mass (zero momentum) reference frame. Two particles ($m_1, m_2$) collide at an angle at respective velocities of $u_1, u_2$. The drawing inherently assumes that the momentum of the 2nd particle is greater than that of the first particle (but of course it could be the reverse or they could even have equal momentums). After the collision, the two particles scatter at angles of $\alpha$ and $\phi$. Because the momentum of particle 1 is greater, I believe it will go to the right and particle 2 to the left. Let's assume that is the case.

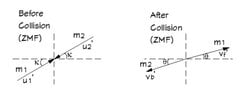
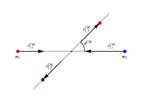
The second diagram converts to the COM or ZMF reference frame. I show what I think the before and after the collision might look like in the COM reference frame. But I'm not sure that these are correct.

My question regards the angles in the COM reference frame. Is the angle of the center of mass only applicable to the drawing that shows after the collision (ZMF)? If so, is it measured from the x axis (as $\theta$ is shown to be) or is it possible that it is measured relative the angle $\kappa$ shown in the before collision (ZMF) drawing? I'm just not sure how the COM angle is defined in this case. Virtually every document or video on this topic (available on the web) is for a situation where $\kappa$ is equal to zero. Also in the lower left quadrant should the angles be shown as $-\kappa$ and $-\theta$ for each drawing respectively?

 

[haruspex]

. Is the angle of the center of mass

Never heard of such a beast. Do you mean the angle of the trajectory of the centre of mass?

, is it measured from the x axis

You are the one coining the term, so define it how you like.

 

[rdemyan]

Yes, the angle of the trajectory of the center of mass. As I understand it, knowing it's value can help in solving for the post collision angles shown on the diagram.

 

[haruspex]

Yes, the angle of the trajectory of the center of mass. As I understand it, knowing it's value can help in solving for the post collision angles shown on the diagram.

Ok, but I still don’t understand your question. You can define its angle as being relative to whatever axis you choose. Are you asking how to calculate it?

 

[rdemyan]

Ok, but I still don’t understand your question. You can define its angle as being relative to whatever axis you choose. Are you asking how to calculate it?

I think I know how to calculate it. The calculation for this case is,

$$\theta_{CM} = tan^{-1} \left(\frac{m_1u_1sin\beta - m_2u_2sin\beta}{m_1u_1cos\beta + m_2u_2cos\beta}\right)$$

Is this calculated trajectory relative to the x axis? Does the angle $\kappa$ have any influence on it? Does the angle $\kappa$ even have any meaning for solving the problem or meaning at all? As I mentioned, all references I have found on the web assume a problem where $\kappa$ is equal to zero. In those web examples, the reason $\kappa$ is equal to zero is because one particle (or sphere) moving along the x axis strikes another particle at rest and then the two particles scatter (see the first attached figure to this reply). There is no angle of collision between the two particles. Surely an angle of collision must impact the results when transforming to the center of mass reference frame? But perhaps the equation posted in this reply already accounts entirely for that influence.

The second attached figure to this reply is a transformation of the first figure into the center of mass frame. The reference states that $\theta_{CM}$ is the scattering angle of particle 1. But isn't this the angle of trajectory of the center of mass as well?

 

[haruspex]

I think I know how to calculate it. The calculation for this case is,

$$\theta_{CM} = tan^{-1} \left(\frac{m_1u_1sin\beta - m_2u_2sin\beta}{m_1u_1cos\beta + m_2u_2cos\beta}\right)$$

Is this calculated trajectory relative to the x axis?

From the fact that you are asking such a question, I surmise that you are quoting a formula given to you, not one you have arrived at for yourself. (We see a lot of that on this forum, students memorising a formula but either not the meanings of the terms or not the circumstances in which it applies.)
The two angles in the formula, $+\beta, -\beta$, are relative to the positive x axis, so $\theta_{CM}$ is too.

Does the angle $\kappa$ have any influence on it? Does the angle $\kappa$ even have any meaning for solving the problem or meaning at all? As I mentioned, all references I have found on the web assume a problem where $\kappa$ is equal to zero. In those web examples, the reason $\kappa$ is equal to zero is because one particle (or sphere) moving along the x axis strikes another particle at rest and then the two particles scatter (see the first attached figure to this reply). There is no angle of collision between the two particles.

Those are matters of reference frame and coordinate choice. $\kappa$ is zero if the choice of coordinates makes it so; one particle starts at rest if the frame of reference makes it so. The two choices are independent.
In your problem, the coordinates chosen have the particles approaching at equal and opposite angles from the x axis. If the momenta of the particles have different magnitudes $\kappa$ will be nonzero.

The second attached figure to this reply is a transformation of the first figure into the center of mass frame. The reference states that $\theta_{CM}$ is the scattering angle of particle 1. But isn't this the angle of trajectory of the center of mass as well?

$\theta_{CM}$ is the change in trajectory of the mass centre. It will equal the final angle of trajectory of the center of mass if the coordinate system is such that the initial angle was zero.

 

[rdemyan]

Let me repeat what you are saying as I understand it, with specific reference to the second figure of my original post. As I understand it, you are saying that $\theta_{CM}$ is the change in trajectory of the center of mass from before the collision to after the collision. So, if the trajectory of the center of mass before the collision is along the angle $\kappa$ (which is defined relative to the x axis), then the trajectory angle of the center of mass after the collision is along the angle $\kappa + \theta_{CM}$ (relative to the x axis).

If I am right, the trick will be to calculate $\kappa$. I've already used all of the initial parameter values (i.e. before the collision), which are known, in order to calculate $\theta_{CM}$ (per the formula in reply#5).

 

[rdemyan]

Okay, but I really don't see how to calculate $\kappa$. If I arbitrarily set $\kappa = 0$, then isn't that similar to rotating the drawing? If I rotate it, then the angles of collision, which are currently $\beta$ and -$\beta$ as shown in the first drawing of the original post, will change (relative to the x axis).

 

[haruspex]

Okay, but I really don't see how to calculate $\kappa$. If I arbitrarily set $\kappa = 0$, then isn't that similar to rotating the drawing? If I rotate it, then the angles of collision, which are currently $\beta$ and -$\beta$ as shown in the first drawing of the original post, will change (relative to the x axis).

Just realised I was confused by the notation. In post #5 you give an expression for $\theta_{CM}$ which is correct for the trajectory of the mass centre (which, of course, is unchanged by the collision). But in the attached picture, $\theta_{CM}$ is shown as the change in the particles' trajectories relative to the mass centre. These are quite different entities.
Which do you want it to mean?

 

[rdemyan]

Thanks for your response. I have also realized that there was confusion. The angle of the center of mass stays constant throughout the collision (both before and after). The $\theta_{CM}$ that was calculated above in the formula is correct. I guess $\kappa$ is largely irrelevant. I may try a different technique to try to solve this problem. One that uses the normal/tangent of the collision and the coefficient of restitution. Tomorrow.