Converting Spherical to Cylindrical Coordinates for a Velocity Expression

[Niles]

Homework Statement

Hi

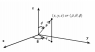
I have an expression on the form
<br /> df(v, \theta, \phi) = v e^{-v^2/C}\cos(\theta)v^2\sin(\theta)\,dv\,d\theta\,d\phi<br />
and I am trying to write it in cylindrical coordinates. Note that θ runs from 0..π, v is a velocity and C a real constant. So I wish to write it in terms of a radial and axial velocity, v_r and v_z.

First I thought of integrating out θ and \phi. \phi is easily done, and it yields 2π. However, the integral over θ yields 0. Am I doing this wrong?

The result should yield something proportional to

<br /> v_re^{-v_r^2/C^2}v_ze^{-v_z^2/C^2}\,dv_r\,dv_z<br />Niles.

 

[marcusl]

In spherical coordinates the integral over theta runs 0 to pi.

 

[Niles]

Hi

Thanks for replying. The integral of cos(theta)sin(theta) over 0..pi gives 0.

 

[marcusl]

Oh, right. I looked at the sin(theta) and didn't see the other term.

 

[Niles]

OK, I am taking a different approach now. Now I use v_r = v\cos(\theta) and v_z = v\sin(\theta). This gives me
<br /> v_rv_zv\,dv\,d\theta<br />
Then I use (from http://en.wikipedia.org/wiki/Spherical_coordinate_system) that \arctan(v_r/v_z) and v=\sqrt(v_r^2+v_z^2) to find dv/dv_r and dθ/dv_z. However, don't get the desired results.

Is my approach wrong?


Niles.

 

[DryRun]

Basically, what you're trying to do is express a complete sphere with radius = v, in terms of cylindrical coordinates, with density v e^{-v^2/C}\cos(\theta). So, forget about the density for now, and focus on the conversion to cylindrical coordinates. Afterwards, plug in the density.

 

[Niles]

Thanks for taking the time to help me. For the conversion I get
<br /> v e^{-v^2/C}\cos(\theta)v^2\sin(\theta) = v_rv_zv e^{-\sqrt{v_r^2+v_z^2}/C}<br />
I have used the relations I linked to above. Can I get a hint to how I should take care of the density?

Best wishes,
Niles.

 

[Niles]

Ahh, I think I get it now. So what you mean is that
<br /> v\,dvd\theta = dv_r\,dv_z<br />

Then it adds up!

 

[HallsofIvy]

In cylindrical coordinates r measures the distance from the origin to the foot of the projection from the point to the xy-plane. The line from the origin to the point in 3 dimensions, the line from the origin to the point at the foot of the projection and the projection form a straight line with hypotenuse of length \rho, angle \pi/2- \phi, "opposite side" of length z, and "near side" of length r. That is, the point that has spherical coordinates \rho, \theta, and \phi has cylindrical coordinates r= \rho sin(\phi), \theta= \theta and z= \rho cos(\phi).

Here, I have used the mathematics convention that \theta is the "longitude" and \phi is the "co-latitude". The physics convention reverses that.

 

[DryRun]

My understanding of the problem is in the attached graph below.
In this problem, \phi is substituted by \theta, \theta is replaced by \phi, and \rho is replaced by v.

So, a description of the sphere would be:
For \phi and \theta fixed, v varies from 0 to v.
For \phi fixed, \theta varies from 0 to ∏.
\phi varies from 0 to 2∏.

The corresponding description in terms of cylindrical coordinates would be:
For \phi and r fixed, z varies from -\sqrt{v^2-v^2\sin^2\theta} to \sqrt{v^2-v^2\sin^2\theta}, where \theta is \arctan ({\frac {r}{z}}).
For \phi fixed, r varies from 0 to v.
\phi varies from 0 to 2∏.

For the integrand:
v e^{-v^2/C}\cos(\theta)Replace \theta by \arctan ({\frac {r}{z}}) and v by \sqrt{r^2+z^2}.

 

[Niles]

Thanks for the help, both of you.Niles.