Simon666
- 93
- 0
Hello,
I am currently trying to simulate an object that can rotate around an axis bouncing on a piece of yarn. I have as equations of motion for the object:
I d²Theta/dt² = Gravity_Torque + Yarn_Torque
With the gravity torque alone this system is perfectly conserving energy: the rotating lever will rotate down from horizontal to horizontal at the other side and back. However, if I also put in the yarn torque, this is only directed upwards, so in my simulations the lever will bounce back from the yarn higher than the position it left from and hence energy is continuously added and my object will bounce back higher and higher. How to solve this issue, what are the correct equations of motion? I'm not so good at physics.
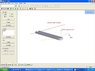
In attachment the situation is displayed.
I am currently trying to simulate an object that can rotate around an axis bouncing on a piece of yarn. I have as equations of motion for the object:
I d²Theta/dt² = Gravity_Torque + Yarn_Torque
With the gravity torque alone this system is perfectly conserving energy: the rotating lever will rotate down from horizontal to horizontal at the other side and back. However, if I also put in the yarn torque, this is only directed upwards, so in my simulations the lever will bounce back from the yarn higher than the position it left from and hence energy is continuously added and my object will bounce back higher and higher. How to solve this issue, what are the correct equations of motion? I'm not so good at physics.
In attachment the situation is displayed.