Correct usage of Gauss's Theorem?

[zorro]

Homework Statement

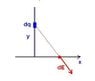
Refer figure.
We have to find the electric field intensity at point O due to a long thread with uniform charge density λ per unit length. R is much less compared to the length of the thread.

The Attempt at a Solution

We can consider a closed Gaussian Cylindrical Surface around the long thread such that the point O lies on it.
Using Gauss's theorem, I found out the electric field intensity at point O as
E = λ/2πεR
This method gives me a wrong result as E is √2λ/4πεR.
Please explain me where am I wrong?

 

[ehild]

Is the point O near the end of the thread?

ehild

 

[zorro]

Yes, the point O is exactly opposite to the lower end of the thread.

 

[ehild]

In this case, the electric field is not radial everywhere, and its intensity also varies along the thread. Integrate the contributions of the elementary charges.

ehild

 

[zorro]

I don't understand how the electric field is not radial. When we derive the the standard equation for the electric field intensity due an infinitely long wire with uniform charge distribution, we take the direction of electric field perpendicular to the line charge (which is radial to a Gaussian Surface imagined), what is different here?

 

[ehild]

The difference is that we are near the end of the the thread, so we can not use the mirror symmetry of an infinite long one. See attachment. A piece of thread with charge dq has a contribution to the electric field shown by the arrow. dE has both radial and y components. The y component would cancel if the thread extended to the negative y direction to negative infinity. But is does not in this case. The Gaussian surface should contain both the wall and the base of that cylinder.

ehild

 

[zorro]

Thanks!