Correspondence Theorem for Groups .... Rotman, Propn 1.82 ....

[Math Amateur]

I am reading the book: "Advanced Modern Algebra" (Second Edition) by Joseph J. Rotman ...

I am currently focused on Chapter 1: Groups I ...

I need help with an aspect of the proof of Proposition 1.82 (Correspondence Theorem) ...

Proposition 1.82 reads as follows:

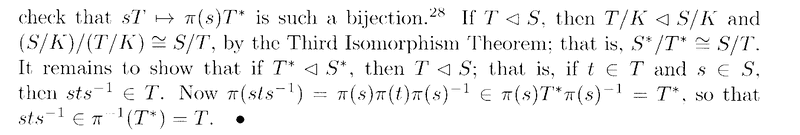
In the above proof by Rotman we read the following:

" ... ... For the reverse inclusion let $a \in \pi^{-1} \pi (S)$, so that $\pi (a) = \pi (s)$ for some $s \in S$. It follows that $as^{-1} \in \text{ ker } \pi = K$ ... ... "Can someone please explain exactly how/why $\pi (a) = \pi (s)$ implies that $as^{-1} \in \text{ ker } \pi = K$ ... ...?Peter

===========================================================================================***EDIT***

Just had some thoughts ... BUT ... unfortunately my logic does not seem to line up with Rotman's logic ...

My thoughts are as follows:

$\pi (a) = \pi (s)$

$\Longrightarrow aK = sK$

$\Longrightarrow a = sk$ for some $k \in K$ since $a$ must belong to $sK$ ... ... (is this a legitimate step ...)

$\Longrightarrow s^{-1} a = k$

$\Longrightarrow as^{-1} = k$

$\Longrightarrow as^{-1} \in \text{ker } \pi = K$Is that correct?

BUT note ... logic is different from Rotman's set of steps ... ... what is Rotman's logic ...?Peter

 

[fresh_42]

$\operatorname{ker}\pi = \{a \in G\,\vert \,\pi(a)=[e] \in G/K\}$ and $[e] \in G/K$ is the coset $e\cdot K$. Important is that $\pi$ is a group homomorphism:
$$
\pi(a)=\pi(s) \Longrightarrow \pi(a)\cdot \pi(s)^{-1}=\pi(as^{-1})=[e] \in G/K \Longrightarrow as^{-1}\in \operatorname{ker}\pi
$$
by definition of the kernel. Now which elements of $G$ map to $G/K \ni [e]= e\cdot K\,$?

 

[Math Amateur]

Hi fresh_42 ... thanks for the help ...

Which elements map to $e_{G/K} = e_{G} K$ ... ?

I think it is all the elements of the normal group $K$ ... Is that correct?

Peter

 

[fresh_42]

Hi fresh_42 ... thanks for the help ...

Which elements map to $e_{G/K} = e_{G} K$ ... ?

I think it is all the elements of the normal group $K$ ... Is that correct?

Peter

Yes.

 

[member 587159]

The canonical map $\pi$ is a homomorphism (easy exercise). Hence, $\pi(a) = \pi(s) \implies \pi(as^{-1}) = \pi(a)\pi(s)^{-1} = e \implies as^{-1} \in \ker \pi$

 

[Math Amateur]

Thanks Math_QED ... most helpful and clear ..

Peter