absolutezer0es
- 14
- 0
Two m = 6.0g point charges on 1.0-m-long threads repel each other after being charged to q = 120nC , as shown in the figure.
What is the angle θ? You can assume that θ is a small angle.
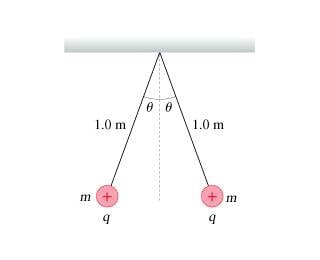
Hopefully the image will work.
I feel like something is missing. I've gotten 7.4 and 3.4 degrees - both wrong. I know the sum of the forces in all directions must equal zero. My equations then are:
Fx = -Tsinθ+Felectric
Fy = Tcosθ - mg
We know m, g, and q. I know that coulomb's law is:
F = Kq^2/r^2 ... but we don't know r.
Any ideas?
What is the angle θ? You can assume that θ is a small angle.
Hopefully the image will work.
I feel like something is missing. I've gotten 7.4 and 3.4 degrees - both wrong. I know the sum of the forces in all directions must equal zero. My equations then are:
Fx = -Tsinθ+Felectric
Fy = Tcosθ - mg
We know m, g, and q. I know that coulomb's law is:
F = Kq^2/r^2 ... but we don't know r.
Any ideas?