Solve Coulomb's Law Problems with Square of Charges | Helpful Tips

[itzxmikee]

Hi guys, these are the final 2 problems that I've been struggling with for the past day. Please help

1. Four point charges are situated at the corners of a square with sides of length a, as in Figure P15.4.

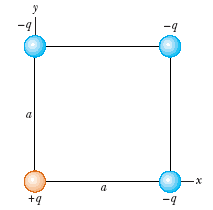
Figure P15.4
Find the expression for the resultant force on the positive charge q.(Use k_e for ke, q for q, and a for a.)



2. Fe = ke(|q||q|/r^2)



3. So I found the x and y components of all the -q. But still get a big sloppy answer.


Question 2

An electron is released a short distance above the surface of the Earth. A second electron directly below it exerts an electrostatic force on the first electron just great enough to cancel the gravitational force on it. How far below the first electron is the second?

Im sure you have to use coulombs law again. But I just don't know where to start with this question.

Thanks guys

 

[Doc Al]

3. So I found the x and y components of all the -q. But still get a big sloppy answer.

What did you get?

Question 2

An electron is released a short distance above the surface of the Earth. A second electron directly below it exerts an electrostatic force on the first electron just great enough to cancel the gravitational force on it. How far below the first electron is the second?

Im sure you have to use coulombs law again. But I just don't know where to start with this question.

What forces act on the first electron? What's the net force on it?

 

[itzxmikee]

What did you get?



What forces act on the first electron? What's the net force on it?

The x components are
-ke(q^2/a^2) - ke(q^2/2a^2)cos45

and the y compents are
-ke(q^2/a^2) - ke(q^2/2a^2)sin45

after simplifications I get the magnitude to be:
sqrt(-2.7keq^2/a^2)

What forces act on the first electron? What's the net force on it?

The forces is weight? mass*gravity?
Net force? weight?

 

[lylos]

What forces act on the first electron? What's the net force on it?

The forces is weight? mass*gravity?
Net force? weight?

It states that the electron below it exerts a force on it great enough to just cancel the force of gravity. So what do we know about the force of gravity and the force due to the electrons repelling each other?

 

[itzxmikee]

It states that the electron below it exerts a force on it great enough to just cancel the force of gravity. So what do we know about the force of gravity and the force due to the electrons repelling each other?

The net force is zero

 

[lylos]

The net force is zero

Great, so when drawing a free body diagram of the electron, you can see that the forces act in two opposite directions, and they must be equal to each other. Using the formulas for the force due to the electron and the force due to gravity, you can then find how far below electron 1 the second electron must be.

 

[itzxmikee]

Ke (q^2)/r^2 = G m^2/r^2

So are we assuming the electrons are the exact mass and charge?
Did I set up the equation right? How do I go about solving for r if I don't know q and m?

 

[lylos]

Now, we're not dealing with the gravitational attraction between the two electrons, rather the electron being pulled to the Earth and then being repelled from the other electron. One side of the equation is correct, the other is not. If you look in your book you should be able to find the charge on an electron and the mass of an electron.

 

[itzxmikee]

Im assuming Ke (q^2)/r^2 is the correct side.
So would it be: Ke (q^2)/r^2 = Ke (q of electron)(q of earth)/r^2

 

[lylos]

Im assuming Ke (q^2)/r^2 is the correct side.
So would it be: Ke (q^2)/r^2 = Ke (q of electron)(q of earth)/r^2

Alright, we have ke (q^2)/(r^2) on the left, and we need to set that equal to the mass of the electron * the acceleration due to gravity.

You sould then have:

Ke (q^2)/(r^2) = m (9.8)

You know Ke, q is the charge of the electron, which should be provided, m, is the mass of the electron, again which should be provided, the 9.8 is the acceleration due to gravity. Now you just solve for r.

 

[itzxmikee]

duhh makes total sense now. Thank you Lylos!

now with the 1st problem. Can anybody help me with that?

 

[lylos]

What you need to do on the first problem is find the X and Y components of the force. Then add them together. For example, the force on q+ due to the q- directly above would be (kqq)/r^2 in the +y direction. Now the force due to the charge to the right would be (kqq)/r^2 in the +x direction. Now the hard part is trying to break down the force due to the charge in the upper right hand corner. It will have an independent x component and an independent y component. Once you have these values you can then find the resultant vector of force.

 

[Doc Al]

The x components are
-ke(q^2/a^2) - ke(q^2/2a^2)cos45

and the y compents are
-ke(q^2/a^2) - ke(q^2/2a^2)sin45

OK:
(1) Realize that \sin (45) = \cos (45) = \sqrt{2}/2
(2) Why negative?

after simplifications I get the magnitude to be:
sqrt(-2.7keq^2/a^2)

I assume you mean: sqrt(2.7)keq^2/a^2

Recheck this; I get a different answer.

 

[itzxmikee]

Okay just looked over the problem again

so I ended up with:

x components:
ke(q^2/a^2) + ke(q^2/2a^2)cos45
=(1+cos45(.5))(ke(q^2/a^2)
= 1.35(ke(q^2/a^2))

and the y components are:
ke(q^2/a^2) + ke(q^2/2a^2)sin45
=(1+sin45(.5))(ke(q^2/a^2)
= 1.35(ke(q^2/a^2))

So to find the magnitude:
((1.35(ke(q^2/a^2))^2 + (1.35(ke(q^2/a^2))^2) ^1/2

am I on the right track?

 

[Doc Al]

Yes, exactly. (Just be careful to square--and square root--things properly: you are missing a few parentheses.)

 

[itzxmikee]

Thanks everyone. Until next time

 

[johnk1317]

Hi I had a question considering this problem. The formula you generate is correct but I don't see how you got it. I will use x to represent the k*q^2/a^2

What I got:
(1+sin45)x for the y axis
(1+cos45)x for the x

What you got:
(1+sin45*.5)x
(1+cos45*.5)x

Where did you derive the .5 from? Thanks for the help.
John

 

[Doc Al]

The formula you generate is correct but I don't see how you got it. I will use x to represent the k*q^2/a^2

Realize that the distance to the charge on the opposite corner is not a, but \sqrt 2a. That's where the .5 comes from.

 

[johnk1317]

Thanks for the clarification