Count the number of automorphisms in the graph

  • Thread starter scorpius1782
  • Start date
  • Tags
    Count Graph
In summary, the conversation is about counting the number of automorphisms in a graph. The person had a previous problem and figured it out, but they want to make sure they are doing this one correctly as well. They mention rearranging elements and come to the conclusion that there are 24 total arrangements. They ask if this is correct, but note that the graph is not attached.
  • #1
scorpius1782
107
0

Homework Statement


I had a different problem before about this and I figured it out. I'd like to know if I'm doing this one correctly as well.
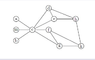
Count the number of automorphisms in the graph.
The graph is attached, now.

The Attempt at a Solution



I know I can rearrange the (a,m,b) 3! ways. I also know that I can only arrange (g,h) and (e,d) 4 ways. So, for each arrangement of (a,m,b) I have 4 arrangements of (g,h) and (e,d). Then 6*4=24 total.

Have I got this sorted out correctly?
 

Attachments

  • graphexample.png
    graphexample.png
    4.8 KB · Views: 493
Last edited:
Physics news on Phys.org
  • #2
Just FYI, the graph is NOT attached.
 
  • Like
Likes 1 person

FAQ: Count the number of automorphisms in the graph

1. How do you define automorphism in a graph?

An automorphism in a graph is a bijective function that maps the vertices of the graph to itself while preserving the structure and connections of the graph. In other words, it is a symmetry or a transformation of the graph that does not change its overall shape or connectivity.

2. What is the importance of counting the number of automorphisms in a graph?

The number of automorphisms in a graph is an important measure of its structural complexity and symmetry. It can provide insights into the underlying patterns and relationships in the graph, which can be useful in various fields such as network analysis, chemistry, and computer science.

3. How do you calculate the number of automorphisms in a graph?

The number of automorphisms in a graph can be calculated using the Polya enumeration theorem or by using special algorithms such as the Nauty algorithm. These methods take into account the symmetries and rotations of the graph to determine the total number of automorphisms.

4. Can the number of automorphisms in a graph be greater than the number of vertices?

No, the number of automorphisms in a graph cannot be greater than the number of vertices. This is because an automorphism is a one-to-one mapping, so it is impossible to map more vertices than the total number of vertices in the graph.

5. What is the relationship between automorphisms and isomorphisms in a graph?

Automorphisms and isomorphisms are closely related concepts in graph theory. An isomorphism is a bijective mapping between two graphs that preserves the edges and vertices, while an automorphism is a special case of an isomorphism where the two graphs are the same. In other words, an automorphism is an isomorphism from a graph to itself.

Similar threads

Domination number of a graph G
Replies
9
Views
1K
Proving a (known isomorphic) graph is isomorphic
Replies
6
Views
2K
Determine limits of integration in double integral change of variables
Replies
2
Views
833
How to show that this expression with tensors reduces to zero?
Replies
6
Views
869
Conditional expectations related to count of event occurring kth time
Replies
2
Views
472
Proving uniqueness of almost irregular graphs with equal degrees for n=2k
Replies
3
Views
2K
Counting the number of set-subset pairs within H
Replies
4
Views
1K
How Does the Graph Laplacian Explain the Multiplicity of Eigenvalue Zero?
Replies
1
Views
1K
Counting problem - how many ways....
Replies
4
Views
3K
Exploring the Automorphism of G with Order 3
Replies
8
Views
1K

Hot Threads

Recent Insights

Back
Top