How Do You Calculate the Counterweight Needed to Balance an L-Shaped Bar?

  • Thread starter Thread starter Alistair Vowles
  • Start date Start date
  • Tags Tags
    Calculation
AI Thread Summary
To calculate the counterweight needed to balance an L-shaped bar, the formula b = ay/x can be used, where 'a' is the force applied at point 'a', 'y' is the length of the bar, and 'x' is the distance from the pivot. For wind resistance, it is suggested to consider the average force applied at y/2 to simplify calculations. It's important to account for a velocity gradient if the structure is tall, as this can affect the force distribution. Additionally, a safety factor of at least double or quadruple the calculated counterweight is recommended to accommodate gusty winds and ensure stability. Proper calculations and safety considerations are crucial for effective balance.
Alistair Vowles
Messages
2
Reaction score
0
I hope this will be an easy one to answer that I could just use a little help with.

I have an L shaped bar where 'X' is on a flat surface. The pivot point is the circle.

Can someone help me with a formula to calculate the force needed at point 'b' , given a certain force applied at point 'a' , to not allow the bar to pivot.

Force 'a' will be a varying force (wind) so I want to make sure I have enough counterweight for force 'b' to allow for this variable.

The fig is not to scale and I plan to have the length of 'X' to be adjustable to decrease the force needed at point 'b' .

I hope this makes sense and thank you for the help !

L bar.jpg
 

Attachments

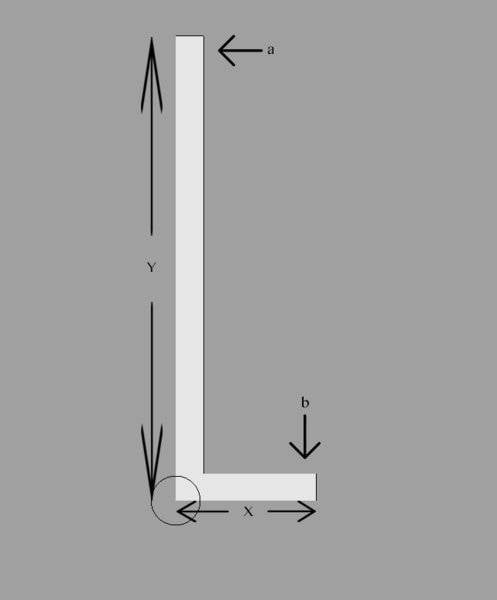
  • L bar.jpg
    L bar.jpg
    7.1 KB · Views: 1,273
Physics news on Phys.org
b=a*y/x
 
If you want an explanation...

If you don't want it to move/accelerate then the net torque must be zero.

Let's define counter clockwise as positive. Then...

ay - bx = 0

Rearrange to give...

ay = bx
Then
b = ay/x
 
Thankyou very much. This is perfect and exactly what I needed.
 
Um, force being wind resistance is spread all the way along y but can be taken as applying at the average point (y/2) (roughly) to simplify the calculation.

So, b = ay/x/2Be aware though that if the base is on the ground or a surface, there is a velocity gradient increasing with distance from the surface which is the reason for (roughly). If the structure is very tall, this could be a significant consideration. If it's an engineering question, you will need at least double, probably quadruple (according to regulation) b to provide a safety factor. This is especially important for aero forces as they are proportional to velocity squared and wind is gusty.

You may already have taken all this into account, it's not stated.
 

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

Fulcrum, balance point and scissor lift force
Replies
2
Views
3K
I [Question] Calculating the force generated by a tarp hung between two walls
Replies
14
Views
2K
Understanding Torque and Reference Frames in Rotational Motion
Replies
4
Views
2K
Forces that act on a physical pendulum
Replies
7
Views
3K
Stress on a spaghetti rod balanced from its middle
Replies
6
Views
1K
Leverage and Forces on a Pivot System
Replies
36
Views
11K
How Do You Calculate Component Forces in an Automotive Drum Brake?
Replies
3
Views
1K
I Simple lateral vehicle dynamics model
Replies
18
Views
3K
A Modeling the damping of a physical rigid pendulum
Replies
1
Views
2K
Can an object maintain uniform motion without any external force?
2
Replies
66
Views
5K

Hot Threads

Recent Insights

Back
Top